\(\mathrm{x}=\sqrt{\mathrm{at}^{2}+2 \mathrm{bt}+\mathrm{c}}\)
Differentiating w.r.t. time
\(\frac{d x}{d t}=v=\frac{1}{2 \sqrt{a t^{2}+2 b t+c}} \times(2 a t+2 b)\)
\(\Rightarrow \mathrm{v}=\frac{\mathrm{at}+\mathrm{b}}{\mathrm{x}}\)
\(\Rightarrow \mathrm{vx}=\mathrm{at}+\mathrm{b}\)
Differentiating w.r.t. \(\mathrm{x}\)
\(\Rightarrow \frac{d v}{d x} \times x+v=a \times \frac{d t}{d x}\)
Multiply both side by v
\(\Rightarrow\left(v \frac{d v}{d x}\right) x+v^{2}=a\)
\(\Rightarrow \mathrm{a}^{\prime} \mathrm{x}=\mathrm{a}-\mathrm{v}^{2}\) [Here \(a'\) is acceleration]
\(\Rightarrow \mathrm{a}^{\prime} \mathrm{x}=\mathrm{a}-\left(\frac{\mathrm{at}+\mathrm{b}}{\mathrm{x}}\right)^{2}\)
\(\Rightarrow \mathrm{a}^{\prime} \mathrm{x}=\frac{\mathrm{ax}^{2}-(\mathrm{at}+\mathrm{b})^{2}}{\mathrm{x}^{2}}\)
\(\Rightarrow \mathrm{a}^{\prime} \mathrm{x}=\frac{\mathrm{a}\left(\mathrm{at}^{2}+2 \mathrm{bt}+\mathrm{c}\right)-(\mathrm{at}+\mathrm{b})^{2}}{\mathrm{x}^{2}}\)
\(\Rightarrow \mathrm{a}^{\prime} \mathrm{x}=\frac{\mathrm{ac}-\mathrm{b}^{2}}{\mathrm{x}^{2}}\)
\(\Rightarrow \mathrm{a}^{\prime}=\frac{\mathrm{ac}-\mathrm{b}^{2}}{\mathrm{x}^{3}}\)
\(\therefore a^{\prime} \propto \frac{1}{x^{3}} \quad \therefore n=3\)
Download our appand get started for free
Similar Questions
- 1$9.8\, {m}$ ઊંચાઈ પર રહેલા નળમાંથી પાણીના ટીપાં જમીન પર પડે છે. ટીપાં એકસરખા અંતરાલમાં પડે છે. જ્યારે પ્રથમ ટીપું જમીન પરે પડે ત્યારે ત્રીજું ટીપું નળમાંથી છૂટે છે. જ્યારે પ્રથમ ટીપું જમીન પર પડે ત્યાર બીજું ટીપું જમીનથી કેટલી ઊંચાઈ ($m$ માં) પર હશે?View Solution
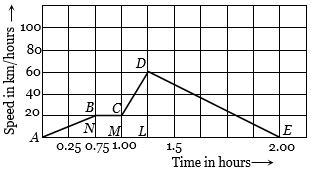
- 2ટ્રેન ના સફર દરમ્યાન મહત્તમ પ્રવેગ કેટલા..........$km h^{-2}$ મળે?View Solution
- 3$h$ ઊંચાઇના ટાવર પરથી એક પદાર્થને $v$ વેગથી ઉપર ફેંકવામાં આવે છે,તો જમીન પર આવતા કેટલો સમય લાગે?View Solution
- 4એક કણનું સ્થાનાંતર $x$ સમય $t$ સાથે $x = a{e^{ - \alpha \,t}} + b{e^{\beta \,t}}$ મુજબ બદલાય છે, જ્યાં $a ,b,\alpha$ અને $\beta$ એ ધન અચળાંક છે. કણનો વેગ ........View Solution
- 5$45\, km/hr$ ની ઝડપથી ગતિ કરતી પોલીસની કાર $153\, km/hr$ ની ઝડપથી ગતિ કરતી ચોરની કારની પાછળ છે.પોલીસ $180\, m/s$ ની ઝડપથી ગોળી છોડે છે.ગોળી ચોરની કારને કેટલા.......$m/s$ ઝડપથી અથડાશે?View Solution
- 6એક કણ $4 \,m$ લંબાઇની નળીમાં $1\, km/sec$ ની ઝડપથી દાખલ થાય છે,અને $9 \,km/sec$ ની ઝડપથી બહાર આવે છે,તો તે નળીમાં કેટલા સમય સુધી રહ્યો હશે?View Solution
- 7એક કણ સીધી રેખા $OX$ પર ગતિ કરે છે. $t ($સેકન્ડમાં$)$ સમયે કણના $O$ થી અંતર $x$ (મીટરમાં) એ $x =40+12 t - t ^{3}$ વડે આપવામાં આવે છે. આ કણ સ્થિર થશે તે પહેલાં કેટલા$.........m$ અંતર કાપશે?View Solution
- 8ધારો કે રબરનો એક દડો $h = 4.9$ મીટર ઊંચાઇથી એક સમક્ષિતિજ સ્થિતિ સ્થાપક પ્લેટ પર મુક્ત રીતે પડે છે. ધારો કે (પ્લેટ સાથેની) અથડામણનો સમય અવગણ્ય છે અને પ્લેટ સાથેની સંઘાત સંપૂર્ણ સ્થિતિસ્થાપક છે. તો સમયનાં વિધેય તરીકે વેગ અને સમયના વિધેય તરીકે ઊંચાઇ કેટલી થશે?View Solution
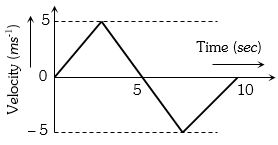
- 9ગતિ કરતા પદાર્થ માટે $v- t$ આલેખ આપેલ છે તો $10\;sec$ સમય દરમિયાન પદાર્થનો સરેરાશ વેગ કેટલો થશે?View Solution
- 10એક પદાર્થ $x=0$ સ્થાને સ્થિર સ્થિતિમાં છે. તે $t=0$ સમયે ધન $x$ દિશામાં અચળ પ્રવેગી ગતિ શરૂ કરે છે. આ જ સમયે બીજો એક પદાર્થ પણ $x =0$ સ્થાનેથી ધન $x$ દિશામાં અચળ ઝડપથી ગતિ કરે છે. $t$ સમય પછી પ્રથમ પદાર્થનું સ્થાન $x _{1}(t)$ વડે તથા સમાન સમય અંતરાલ પછી બીજા પદાર્થનું સ્થાન $x _{2}(t)$ વડે અપાય છે. નીચેનામાંથી ક્યો આલેખ $\left( x _{1}- x _{2}\right)$ ને સમય $t$ ના વિધેય તરીકે સાચી રીતે દર્શાવે છે?View Solution
