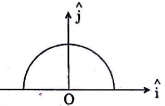
Let us consider a differential element \(d l .\) charge on this element.
\(d q=\left(\frac{q}{\pi r}\right) d l\)
\(=\frac{q}{\pi r}(r d \theta)(\because d l=r d \theta)\)
\(=\left(\frac{q}{\pi}\right) d \theta\)
Electric field at \(O\) due to \(d q\) is
\(d E=\frac{1}{4 \pi \epsilon_{0}} \cdot \frac{d q}{r^{2}}=\frac{1}{4 \pi \epsilon_{0}} \cdot \frac{q}{\pi r^{2}} d \theta\)
The component \(d E \cos \theta\) will be counter balanced by another element on left portion. Hence resultant field at \(\mathrm{O}\) is the resultant of the component \(d E \sin \theta\) only.
\(\therefore E=\int d E \sin \theta=\int_{0}^{\pi} \frac{q}{4 \pi^{2} r^{2} \epsilon_{0}} \sin \theta d \theta\)
\(=\frac{q}{4 \pi^{2} r^{2} \epsilon_{0}}[-\cos \theta]_{0}^{\pi}=\frac{q}{4 \pi^{2} r^{2} \epsilon_{0}}(+1+1)\)
\(=\frac{q}{2 \pi^{2} r^{2} \epsilon_{0}}\)
The direction of \(E\) is towards negative \(y-\) axis.
\(\therefore \vec{E}=-\frac{q}{2 \pi^{2} r^{2} \epsilon_{0}} \hat{j}\)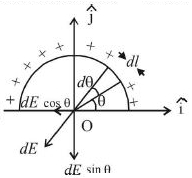
Download our appand get started for free
Similar Questions
- 1અનુક્રમે, $+ \sigma$ અને $+ \lambda$ વિદ્યુતભાર ધનતા ધરાવતા એક અનંત પૃષ્ઠ વિદ્યુતભાર અને અનંત રેખીય વિદ્યુતભારને, એકબીજાને સમાંતર $5\,m$ અંતરે રાખવામાં આવે છે. બિંદુ $P$ અને $Q$ એ રેખીય વિદ્યુતભારથી લંબઅંતરે પૃષ્ઠ તરફ અનુક્રમે $\frac{3}{\pi}\, m$ અને $\frac{4}{\pi}\,m$ અંતરે રહેલા બિંદુ છે. બિંદ્દુ $P$ અને $Q$ આગળ પરિણામી વિદ્યુતક્ષેત્ર ના મૂલ્યો અનુક્રમે $E_P$ અને $E _Q$ છે. જો $2|\sigma|=|\lambda|$ હોય, તો $\frac{E_P}{E_Q}=\frac{4}{a}$ મળે છે. $a$ નું મૂલ્ય ....... થશે.View Solution
- 2જો $\vec p$ ડાઈપોલ મોમેન્ટ ધરાવતા ડાઈપોલને નિયમિત વિદ્યુતક્ષેત્ર $\vec E$ માં મુક્તા તેના પર કેટલું ટોર્ક લાગશે?View Solution
- 3ગાઉસનો નિયમ ${ \in _0}\,\oint\limits_{} {\vec E,\,d\vec s\,\, = \,\,q} $ દ્વારા આપવામાં આવે છે જો ગાઉસિયન પૃષ્ઠ વડે ઘેરાતો ચોખ્ખો વિદ્યુતભાર શૂન્ય હોય તો .......View Solution
- 4$R$ ત્રિજ્યાના અને અનંત લંબાઈના વિદ્યુતભાર વિતરણ વાળા નળાકારને લીધે વિદ્યુતક્ષેત્ર શોધો અને તેની પાસે રેખીય વિદ્યુતભાર ઘનતા $\lambda$ છે. જે તેના અક્ષથી અડધી ત્રિજ્યા આગળ મળે છે.View Solution
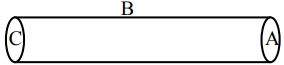
- 5એક પોલા નળાકારમાં $q$ કુલંબ વિદ્યુતભાર રહેલો છે.જો નળાકારની વક્રાકાર સપાટી $B$ સાથે સંકળાયેલ ફલક્સ $\phi \;volt-meter$ હોય, તો સમતલ સપાટી $A$ સાથે સંકળાયેલ ફલક્સ $V-m$ એકમમાં કેટલું હશે?View Solution
- 6View Solutionનીચેનામાંથી કયો વિદ્યુતભાર શકય નથી.
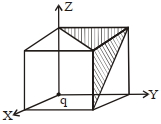
- 7આકૃતિમાં દર્શાવ્યા મુજબ $'q'$ વિજભાર ને સમઘનનાં એક ખૂણા પર ગોઠવવામાં આવ્યો છે. આચ્છાદિત ક્ષેત્રફળમાંથી પસાર થતાં સ્થિત વીજ ક્ષેત્ર $\overrightarrow{ E }$ નું ફ્લક્સ ...... હશે.View Solution
- 8સાચું વિધાન પસંદ કરો.View Solution
$(1)$ બળની વિદ્યુત રેખા ઘનતા આપેલ બિંદુ આગળ વિદ્યુત તીવ્રતા સદિશ $E$ ના મૂલ્યથી સ્વતંત્ર હોય છે.
$(2)$ બળની વિદ્યુત રેખા ઘનતા આપેલ બિંદુ આગળ તેના વિદ્યુત તીવ્રતા સદિશ $E$ ના સમપ્રમાણમાં હોય છે.
$(3)$ વાસ્તવમાં વિદ્યુતક્ષેત્ર રેખાઓ મળતી નથી. તે માત્ર વિદ્યુત ક્ષેત્રની આલેખીય રજૂઆત જ છે.
$(4)$ વાસ્તવમાં વિદ્યુત ક્ષેત્ર રેખાઓ મળે છે.
- 9$1.2 \times 10^{-30} \,Cm$ અને $2.4 \times 10^{-30} \,Cm$ દ્વિ-ધ્રુવી ચાકમાત્રા ધરાવતી બે વિદ્યુત દ્વિ-ધ્રુવીઓને અનુક્રમે બે $5 \times 10^{4}$ $NC ^{-1}$ અને $15 \times 10^{4} \,NC ^{-1}$ જેટલા નિયમીત વિદ્યુતક્ષેત્રમાં મૂકવામાં આવે છે. વિદ્યુત દ્વિ-ધુવીઓ દ્વારા અનુભવતા મહત્તમ ટોર્કનો ગુણોત્તર $\frac{1}{x}$ છે. $x$ નું મૂલ્ય ......... થશે.View Solution
- 10$a$ બાજુવાળા ચોરસ ના શિરોબંદુ પર $+Q$ વિદ્યુતભાર મૂકેલા છે.તો એક વિદ્યુતભાર પર કેટલું બળ લાગે?View Solution
