એક પદાર્થ લાકડાના બ્લોકમાં અંદર જઇને તેનો વેગ અડધો થાય ત્યાં સુધી તે બ્લોકમાં $3\, cm$ જેટલું અંતર કાપે છે. આ પદાર્થ બ્લોકમાં સ્થિર થાય ત્યાં સુધીમાં તે વધારે કેટલું અંતર ($cm$ માં) કાપશે?
AIEEE 2005, Diffcult
b
(b) Let initial velocity of the bullet \(= u\)
(b) Let initial velocity of the bullet \(= u\)
After penetrating \(3\, cm\) its velocity becomes \(\frac{u}{2}\)
From \({v^2} = {u^2} - 2as\)
\({\left( {\frac{u}{2}} \right)^2} = {u^2} - 2a\,(3)\)
\(⇒\) \(6a = \frac{{3{u^2}}}{4}\) \(⇒\) \(a = \frac{{{u^2}}}{8}\)
Let further it will penetrate through distance \(x\) and stops at point \(C\).
For distance \(BC\), \(v = 0,\,u = u/2,\,s = x,\,a = {u^2}/8\)
From \({v^2} = {u^2} - 2as\) \(⇒\) \(0 = {\left( {\frac{u}{2}} \right)^2} - 2\left( {\frac{{{u^2}}}{8}} \right)\,.\,x\) \(⇒\) \(x = 1\,cm\).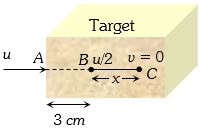
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રથમ $1\ sec$ અને પછીની $2\sec$ ના વેગ નો ગુણોત્તર કેટલો થાય?View Solution
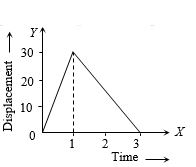
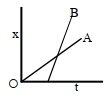
- 2બે વિદ્યાર્થીઓ $A$ અને $B$ નિશાળથી તેમના ઘરે પાછા ફરે છે તે વખતનો સ્થાન-સમય આલેખ આકૃતિમાં દર્શાવ્યો છે.View Solution
નીચે આપેલા વિધાનોમાથી ક્યાં સાચા છે?
$(A)$ $A$ નિશાળથી નજીક રહે છે.
$(B)$ $B$ નિશાળથી નજીક રહે છે.
$(C)$ $A$ ધરે પહોંચવા માટે ઓછો સમય લે છે.
$(D)$ $A$ એ $B$ થી વધુ ઝડપે જાય છે.
$(E)$ $B$ એ $A$ થી વધુ ઝડપે જાય છે.
- 3કણ $x = a + b{t^2}$ મુજબ ગતિ કરે જયાં $a=15\,cm$ અને $b=3\,cm$ તો $t=3\,sec$ કણ નો વેગ કેટલો ..........$cm/sec$ થાય?View Solution
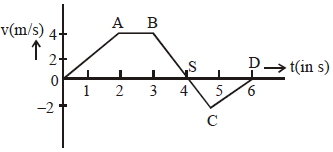
- 4એક સીધી રેખામાં ગતિ કરતાં પદાર્થ માટે વેગ $(v)$ વિરુદ્ધ સમય $(t)$ નો આલેખ આપેલ છે. બિંદુ $S$ એ $4.333$ સેકન્ડ પર છે. પદાર્થે $6 \;s$ માં કાપેલ કુલ અંતર ($m$ માં) કેટલું હશે?View Solution
- 5View Solutionકયો વેગ વિરૂઘ સમય નો ગ્રાફ શકય નથી.
- 6એક બસ $2\,m / s ^2$ ના પ્રવેગથી ગતિ કરે છે. બસથી $96\,m$ પાછળ રહેલો સાયકલ ચલાવનાર બસની સાથે જ $20\,m / s$ થી શરૂઆત કરે છે. $..........\,s$ સમયે તે બસને $Overtake$ કરશે.View Solution
- 7ટાવર પરથી એક પદાર્થને $10 \,m/s$ ના વેગથી નીચે તરફ ફેંકવામાં આવે છે. $3^{rd}\, sec$ અને $2^{nd} \,sec$ માં કાપેલ અંતરનો ગુણોત્તર કેટલો થાય? ($g = 10m/{s^2}$)View Solution
- 8એક કણ ઉદ્ગમ બિંદુથી સ્થિર સ્થિતિમાં $6 m/s^2$ ના પ્રવેગથી $x$ દિશામાં અને $8 m/s^2$ ના પ્રવેગથી $y$ દિશામાં ગતિ કરતો હોય,તો $4 sec$ પછી તેણે કેટલા........$m$ સ્થાનાંતર કર્યું હશે?View Solution
- 9View Solutionનીચેનામાંથી કયો આલેખ એક પરિમાણિક ગતિ દર્શાવતો નથી?
- 10એક કણ સીધી રેખા $OX$ પર ગતિ કરે છે. $t ($સેકન્ડમાં$)$ સમયે કણના $O$ થી અંતર $x$ (મીટરમાં) એ $x =40+12 t - t ^{3}$ વડે આપવામાં આવે છે. આ કણ સ્થિર થશે તે પહેલાં કેટલા$.........m$ અંતર કાપશે?View Solution
