\(X \) અક્ષ દિશામાં રેખીય વેગમાનનું સંરક્ષણ \(mu_1 = mv_1cos \theta _1 + mv2cos \theta_2 ⇒ u_1 = v_1cos \theta_1 + v2cos \theta_2 ……….(i)\)
\(Y \) - દિશામાં રેખીય વેગમાનનું સંરક્ષણ \(0 = mv_1sin \theta _1 - mv_2sin \theta _2 ⇒ 0 = v_1sin \theta_1 - v_2sin \theta_2 ………(ii)\)
ગતીઉર્જા નું સરક્ષણ \(\,\frac{{\text{1}}}{{\text{2}}}mu_1^2\,\, = \,\,\frac{1}{2}mv_1^2\,\, + \,\,\frac{1}{2}mv_2^2\,\,\,\,\, \Rightarrow \,\,\,\,\,u_1^2\,\, = \,\,v_1^2\,\, + \,\,v_2^2\,\,\,\,\,.........(iii)\)
\((i)^2 + (ii)^2 \) પરથી,
\( \Rightarrow \,\,{u_1}^2\,\, + \,\,0\,\, = \,\,{v_1}^2{\cos ^2}{\theta _1}\, + \,\,{v_2}^2{\cos ^2}{\theta _2}\, + \,\,2{v_1}{v_2}\,\cos {\theta _1}\,\cos {\theta _2}\,\, + \,\,{v_1}^2{\sin ^2}{\theta _1}\, + \,\,{v_2}^2{\sin ^2}{\theta _2}\, - \,\,2{v_1}{v_2}\sin {\theta _1}\sin {\theta _2}\)
\( \Rightarrow \,\,{u_1}^2\, = \,\,{v_1}^2({\cos ^2}{\theta _1}\, + \,\,{\sin ^2}{\theta _1})\,\, + \,\,{v_2}^2\,({\cos ^2}{\theta _2}\, + \,\,{\sin ^2}{\theta _2})\,\, + \,\,2{v_1}{v_2}(\cos {\theta _1}\,\cos {\theta _2}\, - \,\,\sin {\theta _1}\,\sin {\theta _2})\)
\( \Rightarrow \,u_1^2\, = \,\,v_1^2\, + \,\,v_2^2\, + \,\,2{v_1}{v_2}\,\cos \,({\theta _1}\, + \,\,{\theta _2})\,\,\,\,\,\,\{ \,\,\because \,\,{u_1}^2\, = \,\,{v_1}^2\, + \,\,{v_2}^2\,\,\} \)
\( \Rightarrow \,\,\cos \,({\theta _1}\, + \,\,{\theta _2})\,\, = \,\,0\,\, \Rightarrow \,\,{\theta _1}\, + \,\,{\theta _2}\,\, = \,\,{90^ \circ }\)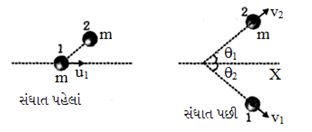
Download our appand get started for free
Similar Questions
- 1$2kg$ ના પદાર્થનો વેગ $36km/h$ છે. $3kg$ ના સ્થિર રહેલા પદાર્થ સાથે અસ્થિતિસ્થાપક સંધાત થાય,તો ગતિઊર્જામાં થતો ઘટાડો.....$J$View Solution
- 2$L = \frac{{10}}{3}\,m$ લંબાઇની દોરી સાથે $1\,kg$ નો પદાર્થ બાંધીને શિરોલંબ વર્તુળાકાર પથ પર ભ્રમણ કરવવામાં આવે છે.દોરીમાં મહત્તમ અને ન્યુનતમ તણાવનો ગુણોત્તર $4$ છે,તો પદાર્થની મહત્તમ ઊંચાઇના બિંદુએ ઝડપ ...... $m/\sec$ હશે.View Solution
- 3એક સાદા લોલકની લંબાઈ $75 cm$ છે. જે શિરોલંબ અર્ધ વર્તૂળ દર્શાવે છે. જ્યારે તે મધ્યવર્તૂળ સ્થાનેથી પસાર થાય ત્યારે દડાનો વેગ કેટલો હશે ?View Solution
- 4$m$ દળનો પદાર્થ $v$ વેગથી તે જ દિશામાં $ kv$ વેગથી જતાં $nm $ દળના પદાર્થ સાથે અથડાતા,પ્રથમ પદાર્થ સ્થિર થાય,તો બીજા પદાર્થનો વેગView Solution
- 5$ {m_A} $ અને $ {m_B} $ દળના વેગ $ {v_A} $ અને $ {v_B} $ છે.અથડામણ પછી $ {m_A} $ અને $ {m_B} $ દળના વેગ $ {v_B} $ અને $ {v_A} $ હોય,તો $ \frac{m_A}{m_B} =$ _____View Solution
- 6$4m$ દ્રવ્યમાનના અને $u$ ઝડપતી ગતિ કરતો એક પદાર્થ $A$ એ $2m$ દ્રવ્યમાનના અને સ્થિર એવા એક પદાર્થ $B$ સાથે અથડાય છે. આ અથડામણ હેડ ઓન અને સ્થિતિસ્થાપક પ્રકૃતિની છે. અથડામણ પછી પદાર્થ $A$ વડે ગુમાવાતી ઊર્જાનો જથ્થો કેટલો હશે?View Solution
- 7$m$ દળનો એક પદાર્થ $v$ વેગથી પ્રારંભમાં સ્થિર સ્થિતિમાં રહેલો $2m$ દળના બીજા પદાર્થ સાથે હેડઓન સંઘાત કરે છે. સંઘાત પહેલા અને સંઘાત પછી સંઘાતી પદાર્થની ગતિ ઊર્જાનો ગુણોત્તર શું હશે ?View Solution
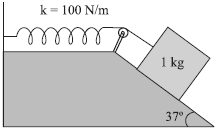
- 8આકૃતિ માં દર્શાવ્યા મુજબ ખરબચડા ઢાળ પર રાખેલ $1\; kg$ નો એક બ્લૉક, $100\;N m ^{-1}$ જેટલા સ્વિંગ અચળાંકવાળી સ્પ્રિંગ સાથે જોડેલ છે. ગિની ખેંચાયા પહેલાંની સામાન્ય પરિસ્થિતિમાં બ્લોકને સ્થિર સ્થિતિમાંથી મુક્ત કરવામાં આવે છે. બ્લૉક સ્થિર સ્થિતિમાં આવતા પહેલાં ઢાળ પર $10 \;cm$ જેટલું નીચે જાય છે. બ્લૉક અને ઢાળ વચ્ચેનો ઘર્ષણ-આંક શોધો. ધારો કે સ્પ્રિંગનું દળ અવગણ્ય છે અને ગરગડી ઘર્ષણરહિત છેView Solution
- 9$m$ દળનો એેક પદાર્થ એ એક દોરીની મદદ વડે $\frac{ g }{6}$ જેટલા અધોગામી પ્રવેગ સાથે અંતર $x$ કાપે તે રીતે છોડવામાં આવે છે. તો દોરી વડે થયેલ કાર્ય છેView Solution
- 10View Solutionનીચેનાં બે વિધાનો પર વિચાર કરો.
1. તંત્રના કણોનું રેખીય વેગમાન શૂન્ય હોય છે.
2. તંત્રના કણોની કુલ ગતિ-ઊર્જા શૂન્ય હોય છે.
