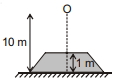
એક પદાર્થને $10 \,m$ ની ઊંંચાઈથી આકૃતિમાં દર્શાવ્યા પ્રમાણે ગતિ કરે છે પદાર્થની અંતિમ $1 \,m$ દરમિયાન ગતિ પર લાગતા સરેરાશ પ્રતિપ્રવેગની ગણતરી કરો.

Medium
b
(b)
(b)
If the ball is dropped then $x=0$, the velocity with which it will hit the sand will be given by
$v^2-u^2=2(-g)(-9)$
$v^2-0=18 g$
$v^2=18 g$
Now on striking sand, the body penetrates into sand for $1 m$ and comes to rest. So, $v \rightarrow$ initial for sand and final velocity $=0$
$v^{\prime 2}-v^2=2(a) \times(-1)$
$\Rightarrow -18 g=-2 a$
$\Rightarrow a=9 g$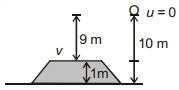
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પદાથૅ સ્થિર સ્થિતિમાંથી $8\,m/{\sec ^2},$ ગતિની શરૂઆત કરે છે.તેને $5^{th}\ sec$ માં કેટલા ..........$metres$ અંતર કાપશે?View Solution
- 2View Solutionમુક્ત પતન કરતા એક પદાર્થ ના પ્રથમ,દ્રિતીય,તૃતીય અને ચોથી સેકન્ડમાં કપાયેલ અંતરોનો ગુણોતર ......... હોય છે.
- 3ગુરુત્વાકર્ષણમાં એક પથ્થર મુકત પતન કરે છે. તે $h_1,h_2 $ અને $ h_3$ અંતર ક્રમશ: પ્રથમ $5$ સેકન્ડમાં, પછીની $ 5 $ સેકન્ડમાં અને પછીની $5$ સેકન્ડમાં કાપે છે. $h_1,h_2 $ અને $h_3$ વચ્ચેનો સંબંધ શું થાય?View Solution
- 4$44.1 \,m$ ઊંચાઇ ધરાવતા એક પુલ ઉપરથી પથ્થરને મુકત કરવામાં આવે છે.$1 \,sec$ પછી બીજા પદાર્થને ફેંકવામાં આવે છે.બંને પદાર્થ પાણીમાં એક સાથે પડે છે.તો બીજા પદાર્થને કેટલા......$m/s$ વેગથી ફેંકયો હશે?View Solution
- 5$\mathrm{Y}-\mathrm{Z}$ સમતલમાં ગતિ કરતી એક કીડીનું સ્થાન ( $\mathrm{S}$ મીટરમાં ) $\mathrm{S}=2 \mathrm{t}^2 \hat{j}+5 \hat{k}$ (જ્યાં $\mathrm{t}$ સેકંડમાં છે) વડે દર્શાવવામાં આવે છે. $t=1 \mathrm{~s}$ વખતે કીડીના વેગના મૂલ્ય અને દિશા _______થશે.View Solution
- 6$50\;km/hr$ ની ઝડપથી જતી કાર બ્રેક માર્યા પછી $6\; m$ અંતર કાપ્યા પછી ઊભી રહે છે. જો $100 \;km/hr$ ની ઝડપથી જતી સમાન કાર માટે લઘુતમસ્ટોપિંગ ડિસ્ટન્સ ($m$ માં) કેટલું થાય?View Solution
- 7એક કાર $150\,km/h$ ની ઝડપથી ગતિ કરે છે અને બ્રેક લગાવ્યા બાદ તે $27\,m$ અંતર કાપીને તે અટકે (સ્થિર) છે. જો આ જ કારે નોંધેલ ઝડ૫ કરતા એક તૃતિયાંશ ઝડપે ગતિ કરતી હોય, તો તે કેટલું અંતર ($m$ માં) કાપીને સ્થિર થશે?View Solution
- 8$u$ વેગથી ફેંકેલો પદાર્થ $T$ સમયમાં મહત્તમ ઊંચાઇ $H$ પર પહોંચે છે.તો નીચેનું વિધાન સાચું છે.View Solution
- 9નીચેનામાંથી ક્યા ઝડપ-સમય $(v-t)$ નો આલેખ ભૌતિક રીતે શક્ય નથી?View Solution
- 10એક કણ સ્થિર સ્થિતિમાંથી અચળ પ્રવેગથી $(p - 1) sec$ માં $s_1$ અંતર અને $p\; sec$ માં ${S_2}$ અંતર કાપતો હોય,તો ${({p^2} - p + 1)^{th}} sec$ માં કેટલું સ્થાનાંતર કરે?View Solution
