એક પેરાશૂટધારી કૂદી પડયા પછી ઘર્ષણરહિત અવસ્થામાં $50 \,m$ જેટલો નીચે આવે છે. ત્યારબાદ પેરેશૂટ ખોલતાં તે $2\, m/s^2$ ના પ્રતિપ્રવેગથી ગતિ કરે છે. તે જમીન પર $3 \,m/s$ ના વેગથી પહોંચે છે. તેણે કેટલી ઊંચાઇએથી ($m$ માં) કૂદકો માર્યો હશે?
AIEEE 2005,AIIMS 2008, Diffcult
a
(a) After bailing out from point \(A\) parachutist falls freely under gravity. The velocity acquired by it will \(‘v’\)
(a) After bailing out from point \(A\) parachutist falls freely under gravity. The velocity acquired by it will \(‘v’\)
From \({v^2} = {u^2} + 2as\) \( = 0 + 2 \times 9.8 \times 50\) \(= 980\)
[As \(u = 0\), \(a = 9.8m/{s^2}\), \(s = 50\, m\)]
At point \(B\), parachute opens and it moves with retardation of 2\(m/{s^2}\) and
reach at ground (Point \(C\)) with velocity of \(3\,m/s\)
For the part \(‘BC’\) by applying the equation \({v^2} = {u^2} + 2as\)
\(v = 3\,m/s\), \(u = \sqrt {980} \,m/s\), \(a = - 2m/{s^2}\), \(s = h\)
\(⇒ {(3)^2} = {(\sqrt {980} )^2} + 2 \times ( - 2)\, \times \,h ⇒ 9 = 980 - 4h\)
\(⇒ h = \frac{{980 - 9}}{4}\) \( = \frac{{971}}{4} = 242.7 \tilde = 243\,m\).
So, the total height by which parachutist bail out = \(50 + 243 = 293\, m\).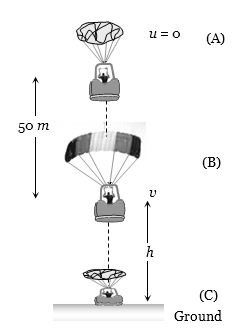
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વિધાન: $M$ અને $m$ દળના $(M > m)$ બે પદાર્થોને સમાન ઊંચાઈએથી પતન કરાવવામાં આવે છે જો હવાનો અવરોધ બંને માટે સરખો હોય તો બંને પદાર્થો એકજ સમયે જમીન પર પહોંચશે.View Solution
કારણ: સમાન હવાના અવરોધ માટે બંને નો પ્રવેગ પણ સમાન થશે.
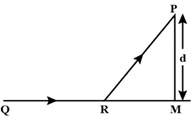
- 2સુરેખ હાઇવે પર એક માણસ કાર લઈને $Q$ સ્થાનેથી $v$ ઝડપથી ગતિ કરે છે. આકૃતિ પ્રમાણે તે હાઇવે (બિંદુ $M$) થી $d$ અંતર દૂર એક વિસ્તારના $P$ સ્થાને જવાનું નક્કી કરે છે. આ વિસ્તારમાં કારની ઝડપ હાઇવે પરની ઝડપ કરતાં અડધી છે. $P$ સ્થાને ન્યુનત્તમ સમયમાં પહોચવા માટે અંતર $RM$ કેટલું હોવું જોઈએ?View Solution
- 3એક ટાવરની ટોચ પરથી એક પથ્થરને પાડવામાં આવે છે તે તેના પતનના અંતિમ સેકેન્ડ દરમિયાન ટાવરની ઊંચાઈના $\left(\frac{5}{9}\right)$ કાપેલ જણાય છે. પતનનો સમય ............. $s$ થાય?View Solution
- 4નિયમિત પ્રવેગ સાથે ગતિ કરતી એક વસ્તુ દ્વારા મેળવવામાં આવતી ગતિ $30\,m / s$ છે જે $2\,sec$ માં મળે છે અને $60\,m /s$ એ $4\,sec$ માં મળે છે. તો પ્રારંભિક વેગ$.............\frac{m}{s}$View Solution
- 5એક ટાવરની ટોચ પરથી ઝડ૫ $u$ સાથે ઉપરથી ફેકવામાં આવે પથ્થર વેગ $4 u$ સાથે જમીન પર પહોંચે છે. ટાવરની ઊંચાઈ ક્ટલી હશે?View Solution
- 6એક બોલ જમીન ઉપર $h$ ઊંચાઈથી છોડવામાં આવે છે. હવાના અવરોધની અવગણના કરો, જમીન પર તેનો વેગ $(v)$ એ તો તેની જમીનથી ઉંચાઈ $(y)$ ની સાપેક્ષે તે કોના તરીકે બદલાય છે?View Solution
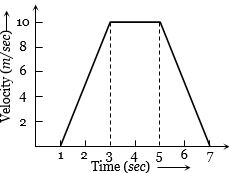
- 7એક પદાર્થનો વેગ વિરુધ્ધ સમયનો આલેખ આપેલ છે.તો પદાર્થે છેલ્લી $2 \,sec$ માં કાપેલ અંતર અને $7 \,sec$ માં કાપેલ અંતરનો ગુણોત્તર કેટલો થાય?View Solution
- 8એક કાર કુલ અંતરના $2/5^{th}$ માં ભાગનું અંતર $v_1$ ઝડપથી અને $3/5^{th}$ માં ભાગનું અંતર $v_2$ ઝડપથી કાપતો હોય,તો સરેરાશ ઝડપ કેટલી થાય?View Solution
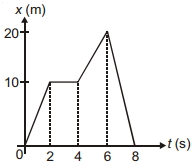
- 9સીધી રેખાની સાપેક્ષે ગતિ કરતાં કણ માટે સ્થાન $(x)$ - સમય $(t)$ નો આલેખ આકૃતિમાં બતાવવામાં આવ્યો છે. સમય અંતરાલ $t=0$ થી $t=8 \,s$ માં કણોની સરેરાશ ઝડપ કેટલી થાય?View Solution
- 10પદાર્થ $A$ અચળ પ્રવેગ $a$ અને પ્રારંભિક વેગ શૂન્ય છે. પદાર્થ $B$ તેજ સ્થાનથી $A$ ની દિશામાં અચળ વેગ $u$ થી ગતિ કરે છે.જો બંને $t$ સમય પછી મળે તો $t=$View Solution
