(b)
Let the total height of tower \(=H\)
Total time of journey \(=t\)
Time taken to cover the \(\frac{5 h}{9}\) is = last second
So, \(s_t-s_{t-1}=\frac{5 h}{9}\)
\(\Rightarrow \frac{1}{2} g t^2-\frac{1}{2} g(t-1)^2=\frac{5}{9} \times \frac{1}{2} g t^2\) \(\left[\because h=\frac{1}{2} g t^2\right]\)
\(\Rightarrow \frac{1}{2} g\left(t^2-t^2-1+2 t\right)=\frac{1}{2} g t^2 \times \frac{5}{9}\)
\(\Rightarrow (2 t-1)=\frac{5}{9} t^2\)
\(\Rightarrow 18 t-9=5 t^2\)
\(\Rightarrow 5 t^2-18 t+9=0\)
\(\Rightarrow 5 t^2-15 t-3 t+9=0\)
\(\Rightarrow 5 t(t-3)-3(t-3)=0\)
\(\Rightarrow(5 t-3)(t-3)=0\)
\(t=\frac{3}{5}, t=3 s \quad\left(t=\frac{3}{5}\right.\), doesn't satisfy the given criterion, so we neglect it)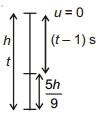
Download our appand get started for free
Similar Questions
- 1એક પદાર્થને ટાવર પરથી $u$ વેગથી ઉપર તરફ ફેંકતા જમીન પર $3u$ વેગથી પહોંચે ,તો ટાવરની ઊંચાઇ કેટલી હશે?View Solution
- 2સીધી રેખાની સાપેક્ષે ગતિ કરતાં કણ માટે સ્થાન $(x)$ અને સમય $(t)$ વચ્ચેનો સંબંધ નીચે આપેલ છે. નીચેના સમીકરણમાંથી કયું એકરૂપ પ્રવેગીય ગતિની રજૂઆત કરે છે? [જ્યાં $\alpha$ અને $\beta$ ધન અચળાંકો છે]View Solution
- 3એક કણ $10.0\,ms ^{-1}$ ના પ્રારંભિક વેગ સાથે $x$-દિશામાં ગતિ શરૂ કેરે છે અને $2.0\,ms ^{-2}$ ના દરે નિયમિત રીતે પ્રવેગિત થાય છે. કણને $60.0\,ms ^{-1}$ ના વેગ સુધી પહોંચવામાં લાગેલો સમય $.......\,s$ છેView Solution
- 4બે કાર $A$ અને $B$ સમાન દિશામાં $30 \,m / s$ અને $20 \,m / s$ વેગ સાથે ગતિ કરી રહી છે. જ્યારે કાર $A$ એ કાર $B$ ની પાછળ $d$ અંતરે હોય ત્યારે, કાર $A$ નો ડ્રાઈવર બ્રેક મારીને $2\, m / s ^2$ નો એકસમાન પ્રતિપ્રવેગ ઉત્પન કરે છે. જ્યારે બંને કાર વચ્ચે કોર અથડામણ નહી થાય ત્યારે,View Solution
- 5એક કણનું સ્થાનાંતર $x$ સમય $t$ સાથે $x = a{e^{ - \alpha \,t}} + b{e^{\beta \,t}}$ મુજબ બદલાય છે, જ્યાં $a ,b,\alpha$ અને $\beta$ એ ધન અચળાંક છે. કણનો વેગ ........View Solution
- 6એક બલૂન $29 \,ms^{-1}$ ના વેગથી ઉપર તરફ ગતિ કરે છે.તેમાંથી પથ્થર મૂકતાં તે $10 \,sec$ માં જમીન તે આવે છે તો બલૂન કેટલી ઊંચાઈએ ($m$ માં) હશે ત્યારે પથ્થર મુક્ત કરવામાં આવ્યો હશે?View Solution
($g = 9.8\,m/{s^2}$)
- 7એક વિદ્યાર્થી બસથી $45\, m$ અંતરે પાછળ ઉભો છે.બસ $2.5 \,m/s^2$ ના પ્રવેગ સાથે ગતિ શરૂ કરે છે.વિદ્યાર્થીને બસ પકડવા માટે કેટલા........$m/s$ લઘુત્તમ અચળ વેગથી દોડવું પડે?View Solution
- 8View Solutionવિધાન:સુરેખ પથ પર કોઈ પદાર્થની નિયમિત ગતિ માટે વેગ-સમય નો આલેખ એ સમય ની અક્ષ ને સમાંતર સુરેખા મળે.
કારણ: નિયમિત ગતિમાં જેમ સમય વીતે તેમ પદાર્થનો વેગ વધતો જાય.
- 9મકાનની ટોચ પરથી એક પથ્થરને મુક્ત કરવામાં આવે છે. જ્યારે આ પથ્થર ટોચથી $5\, m$ નીચે આપેલા બિંદુ પાસેથી પસાર થાય છે, ત્યારે ટોચથી $25\, m$ નીચે રહેલા બિંદુ પરથી બીજા પથ્થરને મુક્ત કરવામાં આવે છે. બંને પથ્થર મકાનનાં તળીયે એક સાથે પહોંચે છે. મકાનની ઊંચાઈ ($m$ માં) કેટલી હશે?View Solution
- 10એક બોલ જમીન ઉપર $h$ ઊંચાઈથી છોડવામાં આવે છે. હવાના અવરોધની અવગણના કરો, જમીન પર તેનો વેગ $(v)$ એ તો તેની જમીનથી ઉંચાઈ $(y)$ ની સાપેક્ષે તે કોના તરીકે બદલાય છે?View Solution
