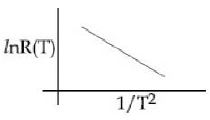
એક પ્રયોગમા અવરોધને તાપમાનના વિધેય તરીકે નીચે મુજબ સીધી રેખા જેવો આલેખ મળે છે.તો નીચેનામાથી શું સાચું હશે?
JEE MAIN 2019, Diffcult
Download our app for free and get started
c
\(\frac{\frac{1}{T^{2}}}{\frac{1}{T_{0}^{2}}}+\frac{\ln R(T)}{\ln R\left(T_{0}\right)}=1\)
\(\frac{\frac{1}{T^{2}}}{\frac{1}{T_{0}^{2}}}+\frac{\ln R(T)}{\ln R\left(T_{0}\right)}=1\)
\(\Rightarrow \ln \mathrm{R}(\mathrm{T})=\ln \mathrm{R}\left(\mathrm{T}_{\mathrm{o}}\right)\left(1-\frac{\mathrm{T}_{\mathrm{o}}^{2}}{\mathrm{T}^{2}}\right)\)
\({\rm{R}}({\rm{T}}) = {{\rm{R}}_0}{{\rm{e}}^{ - \left( {\frac{{T_0^2}}{{{T^2}}}} \right)}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
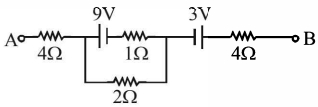
- 1નીચે આપેલા આકૃતિમાં બિંદુ $A$ અને $B$ વચ્ચેનો તફાવત $16\,v$ છે. $2\,\Omega$ માંથી પસાર થતો પ્રવાહ $...........\,A$View Solution
- 2અચળ $e.m.f$ ધરાવતા વિધુત કોષને પહેલા અવરોધ $R_1$ અને ત્યારબાદ અવરોધ $R_2$ સાથે જોડવામાં આવે છે. જો બંને કિસ્સામાં વપરાતો પાવર સમાન હોય તો વિધુતકોષનો આંતરીક અવરોધ કેટલો હશે ?View Solution
- 3$X-ray$ ટયુબમાં વોલ્ટેજ $ 5\, kV $ અને પ્રવાહ $3.2 \,mA $ છે,તો દર સેકન્ડે એનોડ પર અથડાતા ઇલેકટ્રોનView Solution
- 4ઓરડામાં સપ્લાય વોલ્ટેજ $120$ $V$ છે.લેડ વાયરનો અવરોધ $6$ $Ω$ છે.ઓરડામાં $60$ $W$ નો બલ્બ પહેલેથી ચાલુ છે.હવે,બલ્બને સમાંતર $240$ $W$ નું હીટર ચાલુ કરવામાં આવે,તો બલ્બને સમાંતર વોલ્ટેજમાં કેટલા ............. $V$ ઘટાડો થશે?View Solution
- 5સ્તંભ$- I$ એ ધાત્વીય સુવાહકમાં વહેતા પ્રવાહને અનુરૂપ ચોક્કસ ભૌતિક રાશિઓ આપે છે. સ્તંભ$- II$ એ સંકળાયેલ વિદ્યુતીય રાશિઓ ધરાવતા અમુક ગાણિતીય સંબંધો દર્શાવે છે. સ્તંભ$-I$ અને સ્તંભ$-II$ ને યોગ્ય સંબંધોથી મેળવો.View Solution
સ્તંભ $- I$ સ્તંભ$- II$ $(A)$ ડ્રિફટ વેગ $(P)$ $\frac{m}{n e^{2} \rho}$ $(B)$ વિદ્યુતીય અવરોધકતા $(Q)$ $\mathrm{ne} v_{\mathrm{d}}$ $(C)$ શિથીલન સમયગાળો $(R)$ $\frac{\mathrm{eE}}{\mathrm{m}} \tau$ $(D)$ પ્રવાહ ઘનતા $(S)$ $\frac{E}{J}$ - 6આપેલ તારનો કે જેની લંબાઈ $L$ અને ત્રિજ્યાં $R$ હોય તેનો વિશિષ્ટ અવરોધ $\left(S_1\right)$ માપવા માટે વ્હીસ્ટોન બ્રિજના સિધ્યાંતનો ઉપયોગ કરવામાં આવે છે. જો તારનો અવરોધ $X$ હોય ત્યારે વિશિષ્ટ અવરોધ $S_1=X\left(\frac{\pi r^2}{L}\right)$ છે. જો તારની લંબાઈ બમણી કરવામાં આવે તો વિશિષ્ટ અવરોધનું મૂલ્ય ........... થશે.View Solution
- 7$5\,A$ ના ફ્યુઝનો ઉપયોગ કરીને $220\,V$ પર $60\,W$ બલ્બ સલામત રીતે ચલાવી શકાય?View Solution
- 8$4\,\Omega $ અવરોધના ત્રણ તારમાથી સમબાજુ ત્રિકોણ બનાવવામાં આવે છે. બે ખૂણા વચ્ચેનો સમતુલ્ય અવરોધ કેટલો થાય?View Solution
- 9પોટેન્શીયોમીટરના તારની લંબાઈ $100\ cm$ છે અને તેના સ્ટેન્ડ અને સેલ કોષનું $emf\ E$ વોલ્ટ છે. તે જેનો આંતરિક અવરોધ $0.5\, \Omega$ હોય તેવી બેટરીનું $emf$ માપવા માટેનો ઘટક છે. જે સંતુલન બિંદુ ધન છેડાથી $ℓ = 30\, cm$ અંતરે મળતું હોય તો બેટરીનું $emf$ ........છે.View Solution
- 10એક કોષ સમય $t$ માટે $R$ અવરોધમાં પ્રવાહ પસાર કરે છે. હવે એ જ કોષ એટલા જ સમય માટે અન્ય અવરોધ $r$ માંથી પ્રવાહ પસાર કરે છે. જો બંને અવરોધમાં ઉત્પન થતી ઉષ્માનો જથ્થો સમાન હોય તો, કોષનો આંતરિક અવરોધ કેટલો હશે?View Solution