એક રેફ્રિજરેટરનો પરફોમન્સ ગુણાંક $5 $ છે. જો ફ્રીઝરની અંદરનું તાપમાન $ -20^o C$ હોય, તો રેફ્રિજરેટરની બહાર બધી બાજુએ, જયાં ઉષ્મા બહાર ફેંકાય છે, તેનું તાપમાન ........ $^oC$ હશે.
AIPMT 2015, Medium
Download our app for free and get started
b
The coefficient of performance of a refrigerator is
The coefficient of performance of a refrigerator is
\(\alpha = \frac{{{T_2}}}{{{T_1} - {T_2}}}\)
where \(T_1\) and \(T_2\) are the temperatures of hot and cold reservoirs \((in\,kelvin)\) respectively.
\(Here,\alpha = 5,{T_2} = - {20^ \circ }C = - 20 + 273\,K = 253\,K\)
\({T_1} = ?\)
\(\therefore \,\,5 = \frac{{253K}}{{{T_1} - 253\,K}}\)
\(5{T_1} - 5\left( {253\,K} \right) = 253\,K\)
\(5{T_1} = 253\,K + 5\left( {253\,K} \right) = 6\left( {253\,K} \right)\)
\({T_1} = \frac{6}{5}\left( {253K} \right) = 303.6\,K = 303.6 - 273\)
\( = {30.6^ \circ }C \approx {31^ \circ }C\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક આદર્શ વાયુ પ્રારંભિક થર્મોડાયનેમિક્સ અવસ્થા $\left(P _1, V _1, T _1\right)$ થી અંતિમ $\left(P_2, V_2, T_2\right)$ સમીકરણ $PV ^2= C$ ને અનુસરે છે, જ્યાં $C$ એ અચળાંક છે. તો .....View Solution
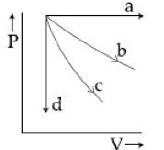
- 2View Solutionઆપેલ ગ્રાફમાં ચાર પ્રક્રિયા આપેલ છે સમકદ,સમદાબી,સમતાપી અને સમોષ્મિ પ્રક્રિયાનો સાચો ક્રમ નીચેનામાથી કયો થશે?
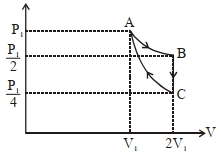
- 3$\left( P _{1}, V _{1}\right)$ એ રહેલ એક મોલ આદર્શ વાયુનું પ્રતિવર્તીય અને સમતાપીય વિસ્તરણ $(A$ થી $B)$ કરાવવામાં આવે, ત્યારે તેનું દબાણ મૂળ દબાણ કરતાં અડધું થાય છે. (આકૃતિ જુઓ) ત્યારબાદ તેનું અચળ કદે ત્યાં સુધી ઠારણ કરવામાં આવે છે કે જેથી તેનું દબાણ મૂળ દબાણ કરતાં ચોથા ભાગનું થાય $( B \rightarrow C )$ ત્યારબાદ પ્રતિવર્તી સમોષ્મી દબાણ દ્વારા $(C$ થી $A)$તેની મૂળ સ્થિતિ પ્રાપ્ત કરવામાં આવે છે. વાયુ દ્વારા થતું ચોખ્ખું કાર્ય ..... છે.View Solution
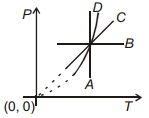
- 4નીચેની આકૃતિ ચાર પ્રક્રિયાઓ $A, B, C, D$ માટે $P-T$ આલેખ દર્શાવે છે. યોગ્ય વિકલ્પ પસંદ કરો.View Solution
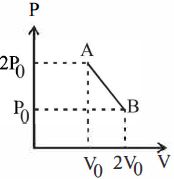
- 5આકૃત્તિમાં દર્શાવ્યા પ્રમાણે, $‘n’$ મોલ આદર્શ વાયુ પ્રક્રિયા $A$$ \to $ $B$ માં પસાર થાય છે. આ પ્રક્રિયામાં આ વાયુનું અધિકતમ તાપમાન હશે.View Solution
- 6પિસ્ટન ઘરાવતા બે પાત્ર $A$ અને $B$ માં એક સમાન વાયુ, $T$ તાપમાન અને $V$ કદ ભરેલો છે.પાત્ર $A$ માં વાયુનું દળ $m_A$ અને પાત્ર $B$ માં વાયુનુ. દળ $m_B$ છે.સમતાપી વિસ્તરણ કરી તેમનું કદ $2V$ કરવામાં આવે છે.પાત્ર $A$ અને $B$ ના દબાણમાં થતો ફેરફાર અનુક્રમે $\Delta P$ અને $1.5 \Delta P$ હોય તોView Solution
- 7$2$ મોલ વાયુનું તાપમાન $340 \;K$ થી $342\; K$ કરતાં આંતરિકઊર્જામાં થતો વધારો ........ $cal.$ ${C_v} = 4.96\,cal/mole\,K$,View Solution
- 8View Solutionએક વાયુ સમોષ્મી રીતે કે સમતાપી રીતે વિસ્તરણ પામી શકે છે. દબાણ અને કદની વિવિધ અવધિ પર બે પ્રક્રિયાઓ માટે સખ્યાંબધ વક્રો દોરવામાં આવે છે તો જોઈ શકાય છે કે
- 9$P$ દબાણ અને $V$ કદના એક પરમાણ્વિક વાયુને પ્રથમ સમતાપીય રીતે વિસ્તરણ કરીને કદ $2V$ સુઘી અને પછી સમોષ્મી રીતે કદ $16 V $ કરે છે. વાયુનું અંતિમ દબાણ કેટલું થશે? ($\gamma = \frac{5}{3}$ લો)View Solution
- 10થરર્મોડાઇનેમિકસ પ્રક્રિયામાં વાયુને $30J$ ઉષ્મા આપવાથી વાયુ દ્વારા થતુ કાર્ય $10J$ છે.શરૂઆતની આંતરિક ઊર્જા $40J$ હોય,તો અંતિમ આંતરિક ઊર્જા ....... $J$ થાય.View Solution