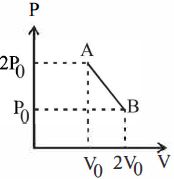
The euatione for the line is
\(P = \frac{{ - {P_0}}}{{{V_0}}}V + 3P\)
\([slope = \frac{{ - {P_0}}}{{{V_0}}},c = 3{P_0}]\)
\(P{V_0} + {P_0}V = 3{P_0}{V_0}\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\)
\(But\,\,\,\,\,\,\,PV = nRT\,\)
\(\therefore P = \frac{{nRT}}{V}\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)\)
\(From\left( i \right)\& \left( {ii} \right)\frac{{nRT}}{V}{V_0} + {P_0}V = 3{P_0}{V_0}\)
\(\therefore nRT{V_0} + {P_0}{V^2} = 3{P_0}{V_0}\)
\(...\left( {iii} \right)\)
For temperature to be maximum \(\frac{{dT}}{{dV}} = 0\)
Differentiating \(e.q.(iii)\,by\,'v'\,we\,get\)
\(nR{V_0}\frac{{dT}}{{dV}} + {P_0}\left( {2v} \right) = 3{P_0}{V_0}\)
\(\therefore nR{V_0}\frac{{dT}}{{dV}} = 3{P_0}{V_0} - 2{P_0}V\)
\(\frac{{dT}}{{dV}} = \frac{{3{P_0}{V_0} - 2{P_0}V}}{{nR{V_0}}} = 0\)
\(V = \frac{{3{V_0}}}{2}\,\,\,\,\,\,\,\,\,\therefore P = \frac{{3{P_0}}}{2}\) \([From (i)]\)
\(\therefore \,{T_{\max }} = \frac{{9{P_0}{V_0}}}{{4nR}}\,\,\left[ {From\,\left( {iii} \right)} \right]\)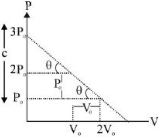
Download our appand get started for free
Similar Questions
- 1ઉષ્મીય એન્જિનને $300 \,cal$ ઉષ્મા આપવામાં આવે છે કે જેથી તે $225 \,cal$ ઉષ્મા ઠારણને આપે છે. જો ઉષ્માપ્રાપ્તિ સ્થાનનું તાપમાન $227^{\circ} C$ હોય તો ઠારણ વ્યવસ્થાનું તાપમાન ........... ${ }^{\circ} C$ હશે.View Solution
- 2ફ્રિજની અંદરનું તાપમાન $ - 13^\circ C. $ છે.તેનો પરફોમન્સ ગુણાંક $5$ છે.તો બહાર ફેંકાતી હવાનું તાપમાન કેટલુ હશે?View Solution
- 3બે કાર્નોટ એન્જિન $A$ અને $B$ નીચે પ્રમાણે કાર્ય કરે છે. $A$ એ $ {T_1} = 800 K $ તાપમાને રહેલા ઉષ્મા પ્રાપ્તિસ્થાનમાંથી ઉષ્મા લઇને $ {T_2} K $ તાપમાનવાળી ઠારણ વ્યવસ્થામાં છોડે છે. $B$ એ $ {T_2} K. $ તાપમાને રહેલા ઉષ્મા પ્રાપ્તિસ્થાનમાંથી ઉષ્મા લઇને $ {T_3} = 300 K. $ તાપમાનવાળી ઠારણ વ્યવસ્થામાં છોડે છે.જો કાર્ય સમાન હોય,તો $ {T_2} =$ ..... $K$View Solution
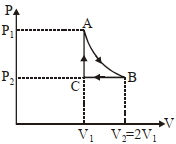
- 4$n$ મોલ ધરાવતાં એક આદર્શવાયું ચક્રિય પ્રક્રિયા $ABCA$ માંથી પસાર થાય છે. (આકૃતિ જુઓ), કે જે નીચેની પ્રક્રિયાઓ ધરાવે છે.View Solution
$A \rightarrow B$ : $T$ તાપમાને સમતાપીય વિસ્તરણકે જેમાં કદ $V _{1}$ થી $V _{2}=2 V _{1}$ બમણું થાય છે અને દબાણ બદલાઈને $P _{1}$ થી $P _{2}$ થાય છે.
$B \rightarrow C$ ; અચળ દબાણ $P _{2}$ એ સમદાબીય સંકોચન દ્વારા પ્રારંભિક કદ $V _{1}$
$C \rightarrow A$ : અચળ કદે કે જે દબાણમાં $P _{2}$ થી $P _{1}$ ફેરફાર કરે છે.
એક પૂર્ણ ચક્રિય પ્રક્રિયા ABCA દરમ્યાન થતું કુલ કાર્ય ,......... થશે.
- 5$T$ તાપમાને રહેલ એક નમૂનાનાં વાયુનું કદ સમોષ્મીય રીતે વિસ્તરણ પામી બમણું થાય છે. આ પ્રક્રિયામાં વાયુ દ્વારા થતું કાર્ય કેટલું હશે? વાયુ માટે સમોષ્મી અચળાંક $\gamma=3 / 2$ છે. $(\mu=1 \text { mole })$View Solution
- 6આદર્શવાયુના એક પ્રયોગ દરમિયાન તે વાયુ એક વધારાના નિયમ $VP^2$ અચળનું પાલન કરતાં જણાય છે. તેનું પ્રારંભિક તાપમાન $T$ અને કદ $V$ છે. જે તેનું કદ વધારીને $2 V$ થાય. ત્યારે અંતિમ તાપમાન કેટલું થશે?View Solution
- 7એક કાર્નોટ એન્જિન કે જેની ઠારણ વ્યવસ્થાનું તાપમાન $27^{\circ} C$ હોય તેની કાર્યક્ષમતા $25 \%$ છે. મૂળ કાર્યક્ષમતાને $100 \%$ જેટલી વધારવા માટે ઉષ્મા ઉદગમનું તાપમાન કેટલા ડીગ્રી જેટલું બદલવું પડશે$?$View Solution
- 8એક મોલ આદર્શ વાયુ $300\; K$ જેટલા અચળ તાપમાને પ્રારંભીક કદ $10$ લીટર થી અંતીમ કદ $20 $ લીટર સુધી પ્રસરણ પામે તો વાયુને પ્રસરવા કરવુ પડતુ કાર્ય ...... $J$ ? $(R = 8.31; J/mole-K)$View Solution
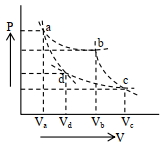
- 9આકૃતિમાં દર્શાવેલ $P-V$ આલેખમાં સમાન વાયુ માટે બે જુદા-જુદા સમોષ્મી પથો બે સમતાપીય વક્રોને છદે છે. $\frac{V_a}{V_d}$ ગુણોત્તર અને $\frac{V_s}{V_c}$ ગુણોત્તર વચ્ચેનો સંબંધ. . . . . . . છે.View Solution
- 10View Solutionસમોષ્મી વિસ્તરણ માટે નીચેનામાથી શું સાચું છે?
