એક સદિશ $\overrightarrow{O A}$ છે જેનું ઉગમ બિંદુ $O$ એ $\overrightarrow{O A}=2 \hat{i}+2 \hat{j}$ મુજબ આપી શકાય. છે. હવે તે વિષમઘડી દિશામાં $45^{\circ}$ ના $1$ ખૂણે $O$ ને અનુલક્ષીને ગતિ કરે, તો નવો સદિશ શું થશે ?
Medium
Download our app for free and get started
a
(a)
(a)
\(\overline{O A}=2 \hat{i}+2 \hat{j}\)
\(|\overline{O A}|=\sqrt{4+4} \Rightarrow 2 \sqrt{2}\)
On rotating by an angle of \(45^{\circ}\) anticlockwise it will lie along \(y\)-axis.
So \(\vec{A}=2 \sqrt{2} \hat{j}\)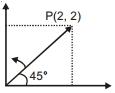
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે સદીશો $\mathop A\limits^ \to \,\, = \,\,3\hat i\,\, + \;\,\hat j\,\,$ અને $\mathop B\limits^ \to \,\, = \,\,\hat j\,\, + \,2\hat k$ આપેલા છે . આ બે સદીશો માટે $\mathop A\limits^ \to $ નો $\mathop B\limits^ \to $ ની સાપેક્ષે ઘટક સદીશના સ્વરૂપમાં શોધો.View Solution
- 2જો $ 0.5\hat i + 0.8\hat j + c\hat k $ એકમ સદિશ હોય, તો $c$ નું મૂલ્ય કેટલું હશે?View Solution
- 3જો $| A + B |=| A |+| B |$ હોય તો સદિશ $ \overrightarrow A $ અને $ \overrightarrow B $ વચ્ચેનો ખૂણો કેટલો હોવો જોઈએ?View Solution
- 4સદિશ $A$ અને $B$ નો પરિણામી સદિશ,સદિશ $A$ ને લંબ છે,અને તેનું મૂલ્ય $B$ સદિશથી અડધું છે,તો સદિશ $A$ અને $ B$ વચ્ચેનો ખૂણો ....... $^o$ થશે.View Solution
- 5બે સદિશો $\vec{A}$ અને $\vec{B}$ નો પરિણામી સદિશ $\vec{A}$ ને લંબ અને તનું મૂલ્ય $\vec{B}$ ના કરતાં અડધુ છે. $\vec{A}$ અન $\vec{B}$ વચ્ચેનો કોણ ............. હશે.View Solution
- 6નીચેનામાંથી કઈ રાશિ/ રાશિઓ યામોક્ષોનાં અભિગમની પસંદગી પર આધાર રાખે છે?View Solution
$(a)$ $\vec{a}+\vec{b}$
$(b)$ $3 a_x+2 b_y$
$(c)$ $(\vec{a}+\vec{b}-\vec{c})$
- 7$5 \,N$ બળ શિરોલંબ સાથે $60^°$ ના ખૂણે લાગે છે,તો બળનો શિરોલંબ ઘટક......... $N$ મેળવો.View Solution
- 8$10$ ન્યુટનનું મૂલ્ય ઘરાવતા $100$ સમતુલ્ય બળો એક પદાર્થ પર લાગે છે.બે બળો વચ્ચેનો ખૂણો $ \pi /50 $ છે. તો પદાર્થ પર લાગતું પરિણામી બળ કેટલા.......... $N$ હશે?View Solution
- 9એક ગતિમાન કણનું કોઈ $t$ સમયે સ્થાન $x = a\, t^2$ અને $y = b\, t^2$ વડે દર્શાવેલ છે. તો કણની ગતિ કેટલી હશે?View Solution
- 10$ABC$ એ સમબાજુ ત્રિકોણ છે. દરેક બાજુની લંબાઈ $'a'$ અને તેનું પરિકેન્દ્ર $O$ છે. $\overrightarrow{A B}+\overrightarrow{A C}=n \overrightarrow{A O}$ હોય તો $n = $ ........View Solution
