For first minimum, the path difference between extreme waves,
\(a \sin \theta=\lambda\)
Here \(\theta=30^{\circ} \Rightarrow \sin \theta=\frac{1}{2}\)
\(\therefore \quad a=2 \lambda\) ..... \((i)\)
For first secondary maximum, the path difference between extreme waves
\(a \sin \theta=\frac{3}{2} \lambda\) or \((2 \lambda) \sin \theta^{\prime}=\frac{3}{2} \lambda\) [Using eqn \((i)\)]
or \(\sin \theta^{\prime}=\frac{3}{4} \quad \therefore \theta^{\prime}=\sin ^{-1}\left(\frac{3}{4}\right)\)
Download our appand get started for free
Similar Questions
- 1નીચે બે કથનનો આપેલ છે.View Solution
કથન $I$ : જો હવામાંથી કાચમાં પ્રસરણ પામતા પ્રકાશ માટે બ્રુસ્ટર કોણ $\theta_{ B }$ હોય, તો કાચમાંથી હવામાં પ્રસરણ પામતા પ્રકાશનો બ્રુસ્ટર કોણ $\frac{\pi}{2}-\theta_B$ છે.
કથન $II$ : કાચમાંથી હવામાં પ્રસરણ પામતા પ્રકાશનો બ્રુસ્ટર કોણ $\tan ^{-1}\left(\mu_{ g }\right)$ છે, જ્યાં $\mu_{ g }$ એ કાચનો વક્રીભવનાંક છે.
ઉપર્યુક્ત બંને કથનના સંદર્ભમાં, નીચે આપેલ વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 2યંગના બે-સ્લિટ પ્રયોગમાં, વપરાતા પ્રકાશની તરંગલંબાઈ $5000 \mathring A$, $0.3 \mathrm{~mm}$ પહોળાઈ ધરાવતી સ્લિટ અને સ્લિટથી પડદો $200 \mathrm{~cm}$ અંતરે રાખવામાં આવેલ છે. મધ્યસ્થ અધિકતમ $x=0 \mathrm{~cm}$ આગળ મળે છે. ત્રીજા ન્યૂનતમ માટે $x$ નું મૂલ્ય. . . . . . . $\mathrm{mm}$ હશે.View Solution
- 3View Solutionબે સમાન પાવર ધરાવતા સોડિયમ લેમ્પમાં વ્યતિકરણની ઘટના અવલોકી શકાતી નથી કારણ કે બન્ને તરંગોને .....
- 4View Solutionબે સુસંબદ્ધ તરંગો .......ધરાવતા હોવા જ જોઈએ.
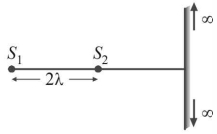
- 5બે સ્ત્રોતને $2 \lambda$ જેટલા અંતરે રાખેલ છે. એક મોટી સ્ક્રીન તેમનો જોડતી રેખાથી લંબ છે. ( $\lambda=$ પ્રકાશની તરંગલંબાઈ) સ્ક્રીન પરના મહત્તમની સંખ્યા ........View Solution
- 6View Solutionનીચેનામાંથી કયો ગુણઘર્મ પ્રકાશનો નથી?
- 7યંગના પ્રયોગમાં બે ઉદ્ગમ વચ્ચેનું અંતર $d=2\lambda$ હોય તો કેટલી મહતમ પ્રકાશિત શલાકા મળે?View Solution
- 8View Solutionવસ્તુનું સ્થાન નક્કી કરવા માટે પ્રકાશનું કિરણપુંજ વાપરવામાં આવે છે. તો ચોક્કસાઈ મેળવવા માટે કેવો પ્રકાશ વાપરવો જોઈએ?
- 9View Solutionહાઈગેનના સિદ્ધાંતનો મુખ્ય ગેરફાયદો.....
- 10$\mu$= $4/3 $ સાબુના પાણીની ફિલ્મ $60^o$ ના ખૂણે આપાત કરેલ સફેદ પ્રકાશથી પ્રકાશિત કરવામાં આવે છે. પરાવર્તિત પ્રકાશમાં $5500\,Å$ તરંગલંબાઈને અનુલક્ષતી ઘેરી પટ્ટી મળે છે. ફિલ્મની ન્યૂનત્તમ જાડાઈ ......$\mathop A\limits^o $ શોધો.View Solution
