એક સમાંતર પ્લેટ કે પેસિટરનું ક્ષેત્રફળ $6\, cm^2$ અને પ્લેટો વચ્ચેનું અંતર $3\,mm$ છે. $K_1 =10, K_2 =12, K_3 =14$ જેટલો પરાવૈધૃતાંક (ડાયઇલેક્ટ્રિક અચળાંક) ધરાવતા અને સમાન જાડાઇ ધરાવતા અવાહક પદાર્થની મદદથી બે પ્લેટો વચ્ચેના ગેપને ભરવામાં આવે છે (આકૃતિ જુઓ). જ્યારે અવાહકને પૂર્ણ તરીકે કેપેસિટરમાં દાખલ કરવામાં આવે અને જો સમાન કેપેસિન્ટસ (સંઘારક્તા) મળે તો પદાર્થનો ડાયઇલેક્ટ્રિક અચળાંક કેટલો હશે.
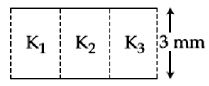

JEE MAIN 2019, Diffcult
c
\(\mathrm{C}_{\mathrm{net}}=\mathrm{C}_{1}+\mathrm{C}_{2}+\mathrm{C}_{3}\)
\(\mathrm{C}_{\mathrm{net}}=\mathrm{C}_{1}+\mathrm{C}_{2}+\mathrm{C}_{3}\)
\(\frac{\mathrm{k} \mathrm{AE}_{\mathrm{o}}}{\mathrm{d}}=\mathrm{k}_{1}\left(\frac{\mathrm{A}}{3}\right) \frac{\mathrm{E}_{\mathrm{o}}}{\mathrm{d}}+\mathrm{k}_{2}\left(\frac{\mathrm{A}}{3}\right) \frac{\mathrm{E}_{\mathrm{o}}}{\mathrm{d}}+\mathrm{k}_{3}\left(\frac{\mathrm{A}}{3}\right) \frac{\mathrm{E}_{\mathrm{o}}}{\mathrm{d}}\)
\(\mathrm{k}=\frac{\mathrm{k}_{1}+\mathrm{k}_{2}+\mathrm{k}_{3}}{3}=12\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે પ્લેટ વચ્યે હવા ધરાવતા સમાંતર પ્લેટ કેપેસીટરનું કેપેસીટન્સ $15\,pF$ છે. જો પ્લેટ વચ્યેનું અંતર બમણું કરવામાં આવે અને તમમાં $3.5$ ડાઈ ઈલેક્ટ્રીક અચળાંકનુ માધ્યમ દાખલ કરવામાં આવે તો કેપેસીટન્સનું મૂલ્ય $\frac{x}{4} pF$ થાય છે. તો $x$ નું મૂલ્ય $..........$ છે.View Solution
- 2$M$ દળનો વિદ્યુતભાર $q$ એ $q$ વિદ્યુતભારની આજુબાજુ સ્થિત વિદ્યુત આકર્ષણને લીધે પરિભ્રમણ કરે છે. તેની ગતિનો આવર્તકાળ..... સૂત્રની મદદથી આપી શકાય છે.View Solution
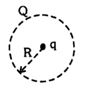
- 3છ વિદ્યુતભાર $+ q ,- q ,+ q ,- q ,+ q$ અને $- q$ ને આકૃતિમાં દર્શાવ્યા મુજબ $d$ બાજુના ષટ્કોણના શિરોબિંદુ પર મૂકેલા છે. અનંતથી ષટ્કોણના કેન્દ્રમાં $q _0$ વિદ્યુતભાર લાવવામાં માટે કેટલું કાર્ય કરવું પડે? $\left(\varepsilon_0-\right.$ મુક્ત અવકાશની પરમિટિવિટી)View Solution
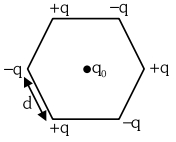
- 4View Solutionખોટું વિધાન શોધો.
- 5એક નળાકારીય કેપેસિટર પાસે $1.4\,cm$ અને $1.5 \,cm$ ત્રિજ્યાના અને $15\,cm$ લંબાઈ ધરાવતા બે નળાકારો છે. બાહ્ય નળાકારને જમીન સાથે જોડેલ છે. અને અંદરના નળાકારને $3.5\ \mu C$ નો વિદ્યુતભાર આપેલ છે. તંત્રનો કેપેસિટન્સ અને અંદરના નળાકારનો સ્થિતિમાન અનુક્રમે. . . . . .View Solution
- 6વિદ્યુતક્ષેત્ર $\mathop E\limits^ \to \,\, = \,\,{e_1}\,\hat i\,\, + \,\,{e_2}\,\hat j\,\, + \,\,{e_3}\,\hat k\,\,\,\,\,\,\,\mathop r\limits^ \to \,\, = \,\,a\,\hat i\,\, + \,\,b\,\hat j\,\,$ મી છે .થતું કાર્ય............છે.View Solution
- 7એક $3\ \mu F$ કેપેસિટરને $300\, V$ ના સ્થિતિમાન સુધી વિદ્યુતભારીત કરેલ છે અને $2\ \mu F$ કેપેસિટરને $200\, V $ સુધી વિદ્યુતભારિત કરેલ છે. ત્યારે કેપેસિટરને અસમાન ધ્રુવીયતા ધરાવતી પ્લેટો સાથે સમાંતરમાં એકબીજા સાથે જોડવામાં આવે છે. જો પ્લેટો આ રીતે જોડેલી હોય, તો કેટલા ......$\mu C$ વિદ્યુતભારનો જથ્થો પસાર થતો હશે ?View Solution
- 8બે બિંદુવત ડાયપોલ ${\vec P_1}$ અને ${\vec P_2}$ એકબીજાથી $x$ અંતરે અને ${\vec P_1}$ || ${\vec P_2}$ છે.આ બંને ડાયપોલ વચ્ચે કેટલું બળ લાગતું હશે?View Solution
- 9પારાના એકસમાન દરેક $512$ ટીપાંઓને $2\, V$ ના સ્થિતિમાનથી વીજભારિત કરવામાં આવે છે. ટીપાંઓને જોડીને એક ટીપું બનાવવામાં આવે છે. આ ટીપાનું સ્થિતિમાન .......... $V$ થશે.View Solution
- 10$C_1$ કેપેસિટન્સવાળા કેપેસિટરને $V$ વોલ્ટ સુઘી ચાર્જ કરેલ છે.આ કેપેસિટરને બીજા વિદ્યુતભાર રહિત $C_2$ ક્ષમતાવાળા કેપેસિટર સાથે સમાંતર જોડવામાં આવે છે. દરેક કેપેસિટર પરના વિદ્યુતસ્થિતિમાનનો તફાવત કેટલો થાય?View Solution
