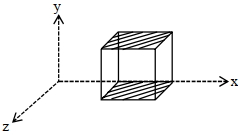
એક સમઘનને $\overrightarrow{{E}}=150\, {y}^{2}\, \hat{{j}}$ જેટલા વિદ્યુતક્ષેત્રની અંદર મૂકવામાં આવે છે. સમઘનની બાજુની લંબાઈ $0.5 \,{m}$ અને તેને આકૃતિમાં દર્શાવ્યા પ્રમાણે મૂકવામાં આવે છે. સમઘનની અંદરનો વિદ્યુતભાર $(\times 10^{-11} {C}$ માં) કેટલો હશે?

JEE MAIN 2021, Diffcult
b
As electric field is in \(y-\)direction so electric flux is only due to top and bottom surface
As electric field is in \(y-\)direction so electric flux is only due to top and bottom surface
Bottom surface \({y}=0\)
\(\Rightarrow {E}=0 \Rightarrow \phi=0\)
Top surface \({y}=0.5\, {m}\)
\(\Rightarrow {E}=150(0.5)^{2}=\frac{150}{4}\)
Now flux \(\phi={EA}=\frac{150}{4}(.5)^{2}=\frac{150}{16}\)
By Gauss's law \(\phi=\frac{Q_{\text {in }}}{\epsilon_{0}}\)
\(\frac{150}{16}=\frac{{Q}_{\text {in }}}{\epsilon_{0}}\)
\({Q}_{\text {in }}=\frac{150}{16} \times 8.85 \times 10^{-12}=8.3 \times 10^{-11} \,{C}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
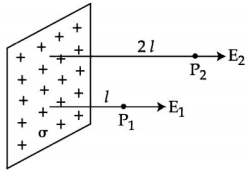
- 1આકૃતિમાં એક ખૂબ મોટું ધન વિદ્યુતભારિત સમતલ પૃષ્ઠ દર્શાવેલ છે. $P _{1}$ અને $P _{2}$ એ વિદ્યુતભાર વિતરણથી $l$ અને $2 l$ જેટલા લઘુત્તમ અંતરે બે બિંદુુઓ છે. જે પૃષ્ઠ વીજભાર ઘનતા $\sigma$ હોય, તો $P_{1}$ અને $P_{2}$ આગળ વિદ્યુતક્ષેત્ર $E_{1}$ અને $E_{2}$ માટે સાચો વિકલ્પ પસંદ કરોView Solution
- 2એક ધન ધાતુના ગોળા પાસે $+ 3Q$ વિદ્યુતભાર છે. જે $-Q$ વિદ્યુતભાર વાળા સુવાહક ગોળીય કવચને સમકેન્દ્રિત છે. ગોળાની ત્રિજ્યા $a$ અને ગોળીય કવચની $b$ છે. $(b > a)$. કેન્દ્રથી $R$ અંતર આગળ $(a < R < b) \,f$ વિદ્યુતક્ષેત્ર ....... છે.View Solution
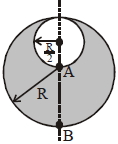
- 3$\mathrm{R}$ ત્રિજ્યા ધરાવતા ગોળા પર વિજભારઘનતા $\rho$ છે.જો તેમાથી $\frac{\mathrm{R}}{2}$ ત્રિજ્યા ધરાવતો ભાગ કાપી નાખવામાં આવે તો $\frac{\left|\overrightarrow{\mathrm{E}}_{\mathrm{A}}\right|}{\left|\overrightarrow{\mathrm{E}}_{\mathrm{B}}\right|}$ નો ગુણોત્તર કેટલો થાય? જ્યાં $\overrightarrow{\mathrm{E}}_{\mathrm{A}}$ અને $\overrightarrow{\mathrm{E}}_{\mathrm{B}}$ બિંદુ $\mathrm{A}$ અને બિંદુ $\mathrm{B}$ પાસે વિદ્યુતક્ષેત્ર છે.View Solution
- 4સમાન વિરૂદ્ધ નિશાની ધરાવતી પૃષ્ઠ વિદ્યુતભાર ઘનતા ($\sigma$ $= 26.4 \times 10^{-12} \ C/m^2$) વાળી બે સમાંતર વિશાળ પાતળી ધાતુની તકતી છે. આ તકતી વચ્ચેનું વિદ્યુતક્ષેત્ર ........$N/C$ છે.View Solution
- 5રેખીય વિદ્યતભાર ઘનતા $\lambda$ ધરાવતી $R$ ત્રિજયાની અર્ધવર્તુળાકાર રીંગના કેન્દ્ર પર વિદ્યુતક્ષેત્ર કેટલું થાય? $\left( {k = \frac{1}{{4\pi {\varepsilon _0}}}} \right)$View Solution
- 6$4\,\mu\,C$ વિદ્યુતભારને બે ભાગ માં વહેંચવામાં આવે છે. જુદા પાડેલા આ બન્ને વિદ્યુતભારો વચ્ચેનું અંતર અચળ છે. જુદા પાડેલ આ વિદ્યુતભારો વચ્ચે લાગતું બળ મહત્તમ થાય તે માટે વિદ્યુતભારોનું મૂલ્ય $..........$ થશે.View Solution
- 7View Solutionજો વિદ્યુતફલક્સ ગાઉસના પૃષ્ઠમાંથી બહાર આવતું હોય તો પૃષ્ઠ સાથે શું સંકળાયેલું હશે ?
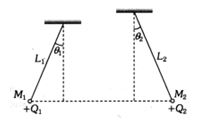
- 8$M_1$ અને $M_2$ દળ ધરાવતા બે નાના ગોળાઓને $L_1$ અને $L_2$ લંબાઇની વજન રહીત અવાહક દોરી વડે લટકાવેલ છે. ગોળાઓ પરનો વિદ્યુતભાર અનુક્રમે $Q_1$ અને $Q_2$ છે. ગોળાઓ એવી રીતે લટકાવેલ છે કે જેથી તેઓ સમક્ષીતીજ એક જ રેખામાં રહે તથા દોરીઓ શીરોલંબ સાથે આકૃતીમાં દર્શાવ્યા મુજબ $\theta_1$ અને $\theta_2$ માપનો ખૂણો બનાવે તો નીચેનામાંથી કઇ શરત $\theta_1$ $=$ $\theta_2$ થવા માટે જરૂરી છે.?View Solution
- 9$2 \,cm$ અને $4 \,cm$ ત્રિજ્યાના બે અલગ કરેલા ગોળાઓમાં સમાન વિદ્યુતભાર આપવામાં આવે છે, તો ગોળાઓની સપાટી પર વિદ્યુતભાર ધનતાનો ગુણોત્તર કેટલો હશે ?View Solution
- 10$10\,cm$ ત્રિજયા ધરાવતા સમાન રીતે વિદ્યુતભારીત અવાહક ગોળાથી $20\,cm$ અંતરે વિદ્યુતક્ષેત્ર $100\, V/m$ છે.તો કેન્દ્રથી $3 \,cm$ અંતરે વિદ્યુતક્ષેત્ર કેટલા .....$V/m$ થાય?View Solution
