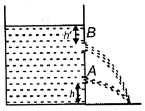
એક ટાંકીએ પાણીથી ભરવામાં આવી છે અને તેની અંદર બે છિદ્રો $A$ અને $B$ પાડવામાં આવે છે. સમાન અવધિ મેળવવા માટે $\frac{h}{h^{\prime}}$ નો ગુણોત્તર કેટલો હોવો જોઇએ ?

Medium
d
(d)
(d)
For hole ' \(A\) '
Velocity of efflux \(=\sqrt{2 g\left(x+h^{\prime}\right)}\)
\(R=2\left[\left(x+h^1\right) h\right]^{1 / 2} \quad \ldots (1)\)
For hole ' \(B\) '
Velocity of efflux \(=\sqrt{2 g h^{\prime}}\)
\(R=2\left[h^{\prime}(x+h)\right]^{1 / 2} \quad \ldots (2)\)
Equating \((a)\) and \((b)\)
We get
\(2\left[\left(x+h^{\prime}\right) h\right]^{1 / 2}=2\left[h^{\prime}(x+h)\right]^{1 / 2}\)
\(\Rightarrow \left(x+h^{\prime}\right) h=h^{\prime}(x+h)\)
\(\Rightarrow h=h^{\prime}\)
\(\Rightarrow \frac{h^{\prime}}{h}=1\)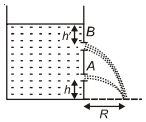
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solution'તરલ' શબ્દનો ઉપયોગ શેના માટે કરવામાં આવે છે ?
- 2હવાનો પરપોટો તળાવમાં તળિયાથી સપાટી સુધી ઉપર ચઢે છે. જો તેની ત્રિજ્યા $200\%$ જેટલી વધે છે અને વાતાવરણનું દબાણ એ $H$ ઊંચાઈના પાણીના સ્તંભ જેટલું છે તો તળાવની ઊંંચાઈ ........ $H$ છે.View Solution
- 3પર્વતના તળિયે અને ઉપર બેરોમીટરમાં મરકયુરીની ઊંચાઇ $75\, cm $ અને $50\, cm$ છે.જો મરકયુરીની અને હવાની ઘનતાનો ગુણોત્તર $10^4$ છે,તો પર્વતની ઊંચાઇ કેટલી હશે?View Solution
- 4એક ટાંકીમાં $20 \,^oC$ તાપમાને ભરેલા તેલમાં થઈને પતન પામતા $ 2.0\, mm$ ત્રિજ્યાના એક કૉપર. બૉલનો અંતિમ વેગ $6.5\, cm\, s^{-1}$ છે. $20 \,^oC$ તાપમાને તેલની શ્યાનતા ગણો. તેલની ઘનતા $1.5 \times 10^3\, kg\, m^{-3}$ છે, તાંબાની ઘનતા $8.9\times 10^3\,kg\,m^{-3}$ છે.View Solution
- 5અનુક્રમે $2 \times 10^{-2}\,m$ અને $4 \times 10^{-2} \,m$ વ્યાસ ધરાવતીને પાણીની પાઈપો $P$ અને $Q$ ને પાણીની મુખ્ય પ્રવાહ રેખા સાથે શ્રેણીમાં જોડવામાં આવે છે. $P$ પાઈપમાંથી વહન થઈ રહેલા પાણીનો વેગ એ .............View Solution
- 6$16 \,cm ^{2}$ જેટલું સમાન આડછેદનું ક્ષેત્રફળ ધરાવતા બે નળાકારીય વાસણો (પાત્રો)માં અનુક્રમે $100 \,cm$ અને $150 \,cm$ ઊંચાઈ સુધી પાણી ભરવામાં આવેલ છે. આ પાત્રોને જોડવામાં આવે છે કે જેથી તેઓમાં પાણીનું સ્તર સમાન ઊંચાઈએ થાય. આ પ્રક્રિયા દરમિયાન ગુરુત્વાકર્ષણને કારણે થતું કાર્ય ..........$J$ થશે. [પાણીની ધનતા $=10^{3} \,kg / m ^{3}$ અને $g =10 \,ms ^{-2}$ લો.]View Solution
- 7$M$ દળ ધરાવતા અને $d$ જેટલી ઘનતા ધરાવતા એક નાના બોલ (દડા) ને, ગ્લીસરીન ભરેલા પાત્રમાં પતન કરવામાં આવે છે ત્યારે તેની ઝડપ અમુક સમય બાદ અચળ થાય છે. જે ગ્લિસરીનની ધનતા $\frac{\mathrm{d}}{2}$ જેટલી હોય તો દડા પર લાગતું સ્નિગ્ધતા (શ્યાનતા) બળ $....$ હશે.View Solution
- 8બાલટીમાં રહેલ પાણીમાં તરતા એક લાકડાના બ્લોકનું $\frac{4}{5}$ ભાગનું કદ પાણીમાં ડૂબેલું છે.જ્યારે બાલટીમાં થોડુક ઓઇલ નાખવામાં આવે ત્યારે બ્લોકનું અડધું કદ પાણીમાં અને અડધું ઓઇલમાં દેખાય છે તો ઓઇલની સાપેક્ષ ઘનતા કેટલી હશે?View Solution
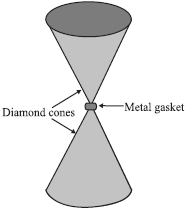
- 9હીરાના એક જ સ્ફટિકમાંથી આકૃતિમાં દર્શાવ્યા મુજબના આકારનું એરણ (anvils) બનાવેલ છે. તેનો ઉપયોગ ઊંચા દબાણ હેઠળ દ્રવ્યની વર્તણૂક તપાસવા માટે થાય છે. એરણના સાંકડા છેડા પાસે સપાટ બાજુઓના વ્યાસ $0.50\, mm$ છે. જો એરણના પહોળા છેડાઓ પર $50,000\, N$ નું દાબીય બળ લાગુ પાડેલ હોય, તો એરણના સાંકડા છેડે (tip) દબાણ કેટલું હશે.View Solution
- 10$10$ સેમી ઊંચાઈ સુધી પાણી ભરેલા પાત્રમાં સપાટી અને તળિયે દબાણનાં તફાવત ..... .View Solution
