હવાનો પરપોટો તળાવમાં તળિયાથી સપાટી સુધી ઉપર ચઢે છે. જો તેની ત્રિજ્યા $200\%$ જેટલી વધે છે અને વાતાવરણનું દબાણ એ $H$ ઊંચાઈના પાણીના સ્તંભ જેટલું છે તો તળાવની ઊંંચાઈ ........ $H$ છે.
Medium
d
(d)
(d)
Let initial radius be \(=r\)
Final radius \(=r+200 \%\) of \(r\)
\(=3 r\)
Atmospheric pressure \(=\rho g H\)
Let depth of the lake be \(h\)
So, pressure at the bottom of lake \(=\rho g H+\rho g h\)
Using \(P_1 V_1=P_2 V_2\)
\(\rho g H \times \frac{4}{3} \pi(3 r)^3=(\rho g H+\rho g h) \times \frac{4}{3} \pi r^3\)
\(\rho g H \times \frac{4}{3} \pi \times 27 r^3=(\rho g H) \frac{4}{3} \pi r^3+\rho g h \times \frac{4}{3} \pi r^3\)
Solving this equation we get
\(26 H=h\)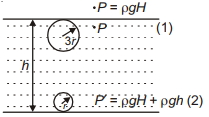
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ઘરની છત પર રહેલી $750\,cm^{2}$ ક્ષેત્રફળ ધરાવતી પાણીની ટાંકીમાં પાણીનું લેવલ પાઈપ ઉપર નળના સ્તરથી ઊંચે રહેલ છે. $500\,nm^2$ આડછેદનું ક્ષેત્રફળ ધરાવતો નળ જ્યારે ખુલ્લો હોય ત્યારે નળમાંથી બાહર નીકળતા પાણીનો વેગ $30\,cm/s$ છે. આ સમયે $\frac{dh}{dt}$ નું મૂલ્ય $x \times 10^{-3}\,m/s$ છે. $x$ નું મૂલ્ય $...........$ હશે.View Solution
- 2$40\; m/s $ ની ઝડપથી ઘરમાં છતને સમાંતર પવન ફૂંકાય છે. છતનું ક્ષેત્રફળ $250 \;m^2$ છે. ઘરમાં દબાણ, વાતાવરણના દબાણ જેટલું ધારીએ તો છત પર પવન દ્વારા લાગતું બળ અને તેની દિશા શું હશે? ($\rho _{air} $ $=1.2 \;kg/m^3$)View Solution
- 3એક શ્યાન પ્રવાહીમાં એક સોનાનાં ગોળાનો ટર્મીનલ વેગ $0.2 \;m / s$ છે. (સોનાની ધનતા $19.5 \;kg / m ^{3}$, શ્યાન પ્રવાહીની ઘનતા $1.5 \;kg / m ^{3}$ ) તો તેટલા જ પરિમાણ વાળા ચાંદીનાં ગોળાનો તે જ પ્રવાહમાં ટર્મીનલ વેગ કેટલો થાય? (ચાંદીની ધનતા $10.5 \;kg / m ^{3}$ છે.)View Solution
- 4$r_1$ અને $r_2$ ત્રિજ્યા અને $l_1$ અને $l_2$ લંબાઈ ધરાવતી બે નળીને શ્રેણીમાં જોડેલ છે અને બંનેમાથી પ્રવાહ ધારારેખી વહન કરે છે. $P_1$ અને $P_2$ એ બે નળીના ચેડાં વચ્ચેનો દબાણ નો તફાવત છે.જો $P_2=4P_1$ અને $l_2= \frac{l_1}{4}$, તો ત્રિજ્યા $r_2$ કેટલી હશે?View Solution
- 5બાલટીમાં રહેલ પાણીમાં તરતા એક લાકડાના બ્લોકનું $\frac{4}{5}$ ભાગનું કદ પાણીમાં ડૂબેલું છે.જ્યારે બાલટીમાં થોડુક ઓઇલ નાખવામાં આવે ત્યારે બ્લોકનું અડધું કદ પાણીમાં અને અડધું ઓઇલમાં દેખાય છે તો ઓઇલની સાપેક્ષ ઘનતા કેટલી હશે?View Solution
- 6$L,\frac{L}{2}$ અને $\frac{L}{3}$ લંબાઈની ત્રણ કેશળીઓ શ્રેણીમાં જોડેલ છે. તેમની ત્રિજ્યાઓ અનુક્કમે $r, \frac{r}{2}$ અને $\frac{r}{3}$ છે. પછી જો ધારારેખીય વહન જાળવી રાખવામાં આવે છે અને પહેલી કેશનળીની વચ્ચે દબાણ $P$ છે તો ...View Solution
- 7પવનની ટનલમાં મોડેલ એરોપ્લેનના ચકાસણી પ્રયોગમાં પાંખની નીચેની અને ઉપરની સપાટી પર વહનની ઝડપ અનુક્રમે $70 \mathrm{~ms}^{-1}$ અને $65 \mathrm{~ms}^{-1}$ છે. જો પાંખનું ક્ષેત્રફળ 2 $\mathrm{m}^2$ હોય તો પાંખની લીફટ __ $N$ છે.View Solution
(હવાની ધનતા = $1.2 \mathrm{~kg} \mathrm{~m}^{-3}$ આપેલ છે)
- 8એક હાઈડ્રોલીક પ્રેસ $100\, kg$ ને ઊંચકી શકે છે જ્યારે $‘m'$ જેટલું દળ નાના પિસ્ટન પર મૂકવામાં આવે છે. દળ ને $‘m’$ જેટલું સમાન રાખીને જો મોટા પીસ્ટનનો વ્યાસ $4$ ગણો વધારવામાં આવે અને નાના પીસ્ટનનો વ્યાસ $4$ ગણો ઘટાડવામાં આવે તો તે ............... $kg$ દળ ઊંચકી શકશે.View Solution
- 9View Solutionપ્રવાહીમાં ધાતુનો નાનો ગોળો નાખતાં તેનો વેગ સમય સાથે કયાં આલેખ મુજબ બદલાય છે. ?
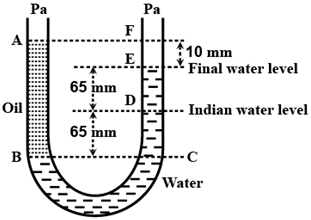
- 10એક $U$ નળી જેના બંને છેડાઓ વાતાવરણ તરફ ખુલ્લા છે, તે આંશિક રીતે પાણીથી ભરેલા છે. પાણી સાથે ન ભળી જાય તેવું તેલ નળીના એક બાજુમાં ત્યાં સુધી ભરવામાં આવે છે, જયાં સુધી બીજી બાજુમાં આવેલા પાણીની સપાટીથી $10\;mm$ ઊંચાઇ પ્રાપ્ત કરી લે છે. આ દરમિયાન પાણી પોતાનો સ્તર $65 \;mm$ જેટલું વધે છે (આકૃતિ જુઓ). તેલની ઘનતા ($kg/m^3$ માં) કેટલી હશે?View Solution