એક ટેબલ પરથી એક પદાર્થને $4 \,m/sec$ ના સમક્ષિતિજ વેગથી ફેંકતા તે જમીન પર $0.4\, sec$ એ આવે છે,તો નીચેનામાંથી શું સાચું છે .
Diffcult
d
(d) Vertical component of velocity of ball at point P
\({v_V} = 0 + gt = 10 \times 0.4 = 4\,m/s\)
Horizontal component of velocity = initial velocity
\( \Rightarrow {v_H} = 4\,m/s\)
So the speed with which it hits the ground
\(v = \sqrt {v_H^2 + v_V^2} = 4\sqrt 2 \,m/s\)
and \(\tan \theta = \frac{{{v_V}}}{{{v_H}}} = \frac{4}{4} = 1\)
(d) Vertical component of velocity of ball at point P
\({v_V} = 0 + gt = 10 \times 0.4 = 4\,m/s\)
Horizontal component of velocity = initial velocity
\( \Rightarrow {v_H} = 4\,m/s\)
So the speed with which it hits the ground
\(v = \sqrt {v_H^2 + v_V^2} = 4\sqrt 2 \,m/s\)
and \(\tan \theta = \frac{{{v_V}}}{{{v_H}}} = \frac{4}{4} = 1\)
\( \Rightarrow\) \(\theta = 45^\circ \)
It means the ball hits the ground at an angle of \(45^\circ \) to the horizontal.
Height of the table \(h = \frac{1}{2}g{t^2} = \frac{1}{2} \times 10 \times {(0.4)^2} = 0.8\,m\)
Horizontal distance travelled by the ball from the edge of table \(h = ut = 4 \times 0.4 = 1.6\,m\)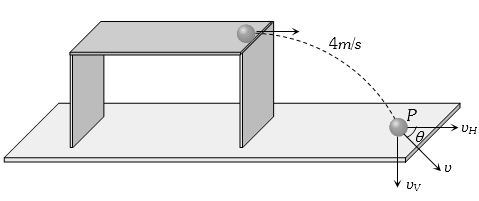
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક કણ $25\, cm$ ત્રિજ્યા વાળા એક વર્તુળમાં $2$ ભ્રમણ/સેકન્ડ ના દરે ગતિ કરે છે. તો કણનો $meter/second^2$ માં પ્રવેગ કેટલો થાય?View Solution
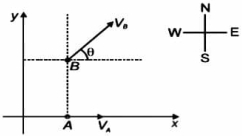
- 2આકૃતિમાં બે જહાજો $x-y$ સમતલમાં $V_A$ અને $V_B$ વેગ સાથે ગતિ કરી રહ્યા છે. જહાજો એવી રીતે ગતિ કરી રહ્યા છે જેથી $B$ હમેશા $A$ ના ઉત્તરમાં રહે.તો $\frac{V_A}{V_B}$ નો ગુણોત્તર શું થશે ?View Solution
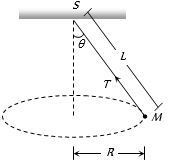
- 3આકૃતિમાં $M$ દળનો પદાર્થ $2/\pi $ પરિભ્રમણ$/sec$ ની કોણીય ઝડપથી ભ્રમણ કરે છે, તો દોરીમાં ઉત્પન્ન થતું તણાવબળ કેટલું હશે?View Solution
- 4સ્થિર સ્થિતિમાંથી $5 \,sec$ માં $20 \,rad/sec$ નો કોણીય વેગ પ્રાપ્ત કરવા પૈડાએ કેટલા પરિભ્રમણ પૂર્ણ કરવા પડે?View Solution
- 5એક બોટ $8\, km/h$ ના વેગ સાથે નદી પાર કરે છે. જો બોટનો પરિણામી વેગ $10\, km/h$ હોય, તો નદીના પાણીનો વેગ ($km/h$ માં) કેટલો હશે?View Solution
- 6$xy-$ સમતલમાં ગતિ કરતાં કણનું સ્થાન સમય $t$ ના પદમાં $x = (3{t^2} - 6t)$ મીટર , $y = ({t^2} - 2t)$ મીટર મુજબ આપવામાં આવે છે. તો ગતિ કરતાં કણ માટે નીચેનામાંથી કયું વિધાન સાચું હશે?View Solution
- 7$100 \,m$ દૂર બંદુક દ્વારા નિશાનને અથડાવવા માટે ગોળીને ........ $cm$ ઊંચાઇ પરથી છોડવી જોઇએ. ગોળીનો સમક્ષિતિજ વેગ $500 \,ms^{-1}$ છે. $( g = 10 \,ms^{-2})$View Solution
- 8View Solutionઅચળ મુલ્યનું બળ બે કણની ગતિની દિશાને લંબ લાગે છે, તો પછી તેની
- 9$1.6 \,m$ લંબાઇની દોરી સાથે પાણી ભરેલું પાત્ર બાંઘીને શિરોલંબ સમતલમાં ભ્રમણ કરાવતા પાણી ઢોળાઇ નહિ તે માટે તેનો વેગ કેટલા.........$m/\sec $ રાખવો જોઇએ? $( g = 10 \,m/sec^2)$View Solution
- 10જહાજ $A$ એ ઉત્તર-પૂર્વ દિશામાં $\vec v = 30\,\hat i + 50\hat j\,km/hr$ વેગ થી સફર કરે છે. જ્યાં $\hat i$ એ પૂર્વ દિશા અને $\hat j$ એ ઉત્તર દિશા સૂચવે છે. જહાજ $A$ થી $80\, km$ દૂર પૂર્વ અને $150\, km$ દૂર ઉત્તર માં જહાજ $B$ એ પશ્ચિમ તરફ $10\, km/hr$ ની ઝડપે સફર કરે છે. $A$ એ $B$ થી ન્યુનત્તમ અંતરે કેટલા .......... $hrs$ પહોચશે?View Solution
