એક તકતી અને એક ગોળાની ત્રિજયા સમાન પણ દ્રવ્યમાન જુદા છે તે સમાન ઊંચાઇ અને લંબાઇના બે ઢાળ પરથી ગબડે છે. બેમાંથી કયો પદાર્થ તળિયે પહેલો પહોંચશે?
NEET 2016, Medium
a
Time taken by the body to reach the bottom when it rolls down an inclined plane without slipping is given by
Time taken by the body to reach the bottom when it rolls down an inclined plane without slipping is given by
\(t = \sqrt {\frac{{2l\left( {1 + \frac{{{k^2}}}{{{R^2}}}} \right)}}{{g\sin \theta }}} \)
Since g is constant and I, R and sin \(\theta \) are same for both
\({{{t_d}}}{{{t_s}}} = \frac{{\sqrt {1 + \frac{{k_d^2}}{{{R^2}}}} }}{{\sqrt {1 + \frac{{k_s^2}}{{{R^2}}}} }} = \sqrt {\frac{{1 + \frac{{{R^2}}}{{2{R^2}}}}}{{1 + \frac{{2{R^2}}}{{5{R^2}}}}}}\)
\({{k_d} = \frac{R}{{\sqrt 2 }},{k_s} = \sqrt {\frac{2}{5}} R}\)
\(= \sqrt {\frac{3}{2} \times \frac{5}{7}} = \sqrt {\frac{{15}}{{14}}} \Rightarrow {t_d} > {t_s}\)
Hence, the sphere gets to the bottom first.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક હળવી દોરીને $5\,kg$ દળ અને $70\,cm$ ત્રિજ્યા ધરાવતા એક પોલા નળાકારની આસપાસ વીટાળવામાં આવે છે. દોરીને $52.5\,N$ બળ વડે ખેંચવામાં આવે છે. નળાકારનો કોણીય પ્રવેગ .......... $rad\,s ^{-2}$ હશે.View Solution
- 2$M$ દળ અને $L$ લંબાઈના તારને અર્ધવર્તુળમાં વાળતા કેન્દ્રમાંથી પસાર થતી અને સમતલને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્રા શું હશેView Solution
- 3View Solutionએક નક્કર ગોળો અવકાશમાં ચાકગતિ કરી રહ્યો છે, જો ગોળાનું દળ અચળ રાખીને તેની ત્રિજ્યા વધારવામાં આવે, તો નીચેનામાંથી કઈ ભૌતિક રાશિ બદલાશે નહિ ?
- 4$5 \mathrm{~kg}$ દળ ધરાવતો પદાર્થ $3 \sqrt{2} \mathrm{~ms}^{-1}$ ની સમાન ઝડપ સાથે $X-Y$ સમતલમાં $y=x+4$ રેખાની દિશામાં ગતિ કરે છે. ઉગમબિંદુને અનુલક્ષીને કણનું કોણીય વેગમાન__________$\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-1}$ થશે.View Solution
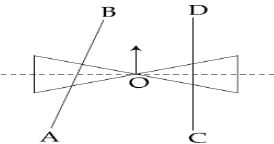
- 5બે શંકુઓને બિંદુ $O$ સાથે જોડીને એક રોલર બનાવવામાં આવેલ છે જેને બે પાટા $AB$ અને $CD$ પર અસંમિત રીતે રાખેલ છે. (જુઓ આકૃત્તિ ), રોલરની અક્ષ $CD$ ને લંબ તથા કેન્દ્ર $O$ એ $AB$ અને $CD$ ને જોડતી રેખાની મધ્યમાં છે. હલકો ધકકો દેતાં રોલર આકૃત્તિમાં બતાવ્યા પ્રમાણે ગતિ કરવાનું શરૂ કરે છે. જયાં કેન્દ્ર $O$ $ CD $ ને સમાંતર ગતિ કરે છે.આમ ગતિ કરતાં રોલરView Solution
- 6તકતીની $R_1$ અને $R_2$ આંતરીક અને બાહ્ય ત્રિજ્યા છે. તે અચળ કોણીય ઝડપ થી સરક્યા વિના ગબડે છે. રિંગના અંદર અને બહારના ભાગ પર રહેલા બે કણો દ્વારા અનુભવાતા બળનો ગુણોત્તર $F_1$/$F_2$ શું થશે ?View Solution
- 7$m$ દળના એક દઢ પદાર્થનું કોઈ એક અક્ષ ફરતે કોણીય વેગમાન તેના રેખીય વેગમાન $(P)$ થી $n$ ગણું છે. આ દઢ પદાર્થની કુલ ગતિઊર્જા કેટલી હશે?View Solution
- 8એક નક્કર પદાર્થ સ્થિર અક્ષને અનુલક્ષીને એવી રીતે ચાકગતિ કરે છે કે જેથી કરીને તેનો કોણીય વેગ $\theta$ પર $\omega=k \theta^{-1}$ મુજબ આધાર રાખે છે, કે જ્યાં $k$ એ ધન અચળાંક છે. જો $t=0$ પર $\theta=0$ હોય તો, $\theta$ નો સમય પર આધાર કેવી રીતે રજૂ કરવામાં આવે છે?View Solution
- 9બે સમાન તકતીના સમતલ એકબીજાને લંબ છે.તેમની કોણીય ઝડપ $3 \,rad/sec $અને $4\,rad/sec$ છે.તો તંત્રની પરિણામી કોણીય ઝડપ ........ $rad/sec$ થાય.View Solution
- 10$m=M$ દળનો પદાર્થ મુકત કરતાં,તે કેટલા પ્રવેગથી ગતિ કરશેView Solution