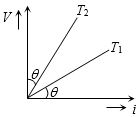
અવરોઘ \( \propto T\)
\(R_1 \propto T_1 ==> tan \theta \propto kT_1 ==> tan \theta = kT_1\) ……. \((i)\)
\(R_2 \propto T_2 ==> tan (90° -\theta) ) T_2 ==> cot \theta = kT_2 \)……..\((ii)\)
\(k({T_2} - {T_1}) = (\cot \theta - \tan \theta )\,\)
\(\,({T_2} - {T_1}) = \left( {\frac{{\cos \theta }}{{\sin \theta }} - \frac{{\sin \theta }}{{\cos \theta }}} \right) = \frac{{({{\cos }^2}\theta - {{\sin }^2}\theta )}}{{\sin \theta \cos \theta }} = \frac{{\cos 2\theta }}{{\sin \theta \cos \theta }} = \cot 2\theta \)
\(==> (T_2 -T_1) )\,\propto\, cot 2\theta\)
Download our appand get started for free
Similar Questions
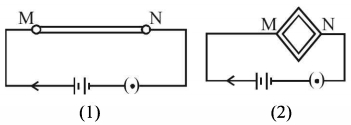
- 1આકૃતિ $(1)$ માં બતાવ્યા મુજબ બિંદુ $M$ એ $N$ વચ્ચેના વાયરને બેટરી સાથે જોડેલ છે. આકૃતિ $(2)$ મુજબ તે વાયરને ચોરસના રૂપમાં વાળીને બે બિંદુઓ વચ્ચેથી બેટરી સાથે જોડેલ છે. નીચેનામાથી કઈ રાશિમાં વધારો થશે.View Solution
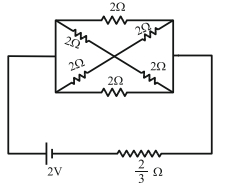
- 2નીચે દર્શાવેલ વિદ્યુત પરિપથમાં બેટરીનું emf $2 \mathrm{~V}$ અને આંતરિક અવરોધ $\frac{2}{3} \Omega$ છે. તો આ સંપૂર્ણ વિદ્યુત પરિપથમાં વપરાતો વિદ્યુત પાવર ...... $W$View Solution
- 3$100\, watt,\,\,220\, volts $ અને $200 \,watt,\,\,220\, volts$ ના બલ્બને શ્રેણીમાં $220\, volts $ ના વોલ્ટ પર લગાવતાં કુલ કેટલા ........ $watt$ પાવર વપરાય?View Solution
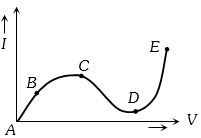
- 4આકૃતિમાં બતાવ્યા પ્રમાણે પ્રવાહ $I$ અને વોલ્ટેજ $V$ વચ્ચે દોરેલા ગ્રાફમાંથી ગ્રાફનો કયો વિભાગ ઋણ અવરોઘ દર્શાવે છેView Solution
- 5ઈલેક્ટ્રિક કીટલીમાં સ્વિચ ઓન (ચાલુ) કર્યા બાદ $20$ મિનિટમાં પાણી ઉકળે છે. જો તે જ મેઈન સપ્લાયનો ઉપયોગ કરી પાણીને $15$ મિનિટમાં ઉકાળવું હોય તો હીટર ઘટકની લંબાઈ મૂળ લંબાઈના. . . . . .ગણી . . . . .પડે છે.View Solution
- 6કોષનો $e.m.f.$ માપવા વોલ્ટમીટર કરતાં પોટેન્શિયોમીટરની પસંદગી વધારે યોગ્ય છે તેના માટેના કારણો નીચે આપેલા છેView Solution
$(i)$ પોટેન્શિયોમીટરમાં કોષમાં કોઈ પ્રવાહ વહેતો નથી.
$(ii)$ પોટેન્શિયોમીટરની લંબાઈના કારણે વધારે સચોટ મૂલ્ય મળે.
$(iii)$ પોટેન્શિયોમીટર દ્વારા ઝડપથી માપન થઈ શકે.
$(iv)$ પોટેન્શિયોમીટરનો ઉપયોગ કરતી વખતે ગેલ્વેનોમીટરની સંવેદિતાથી કોઈ ફરક પડતો નથી
ઉપર પૈકી કયા કારણો સાચા છે?
- 7$E\,\ e.m.f.$ વાળા બેટરી અવરોધ $R$ અને વોલ્ટમીટર $a$ સાથે શ્રેણીમાં જોડેલી છે. એમીટર બેટરી સાથે સમાંતરમાં જોડેલું છે. તો...View Solution
- 8View Solutionબે સમાન લંબાઈના હીટર વાયરને પહેલા શ્નેણીમાં અને પછી સમાંતરમાં જોડવામાં આવે છે.બંનેમાં ઉત્પન્ન થતી ઉષ્માનો ગુણોતર કેટલો થાય?
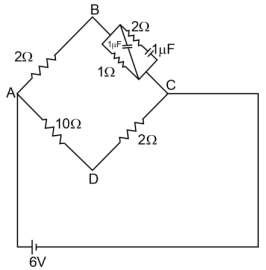
- 9આપેલ પરિપથ. માટે, સ્થાયી સ્થિતિમાં, $\left|V_B-V_D\right|=...........V.$View Solution
- 10$1\, \Omega$ આંતરિક અવરોધ અને $5\, {V}\; emf$ ધરાવતા પાંચ સમાન કોષોને $R$ જેટલા બાહ્ય અવરોધ સાથે શ્રેણીમાં અને સમાંતરમાં જોડેલા છે. $R$ ($\Omega$ માં) ના કયા મૂલ્ય માટે શ્રેણી અને સમાંતરમાં સમાન પ્રવાહનું વાહન થાય?View Solution
