એક વ્હીસ્ટન બ્રિજની ચાર ભુજાઓ $P,Q,R$ અને $S$ ના અવરોધો અનુક્રમે $10\,Ω,\,30\,Ω,\,30\,Ω $ અને $90\,Ω$ છે.કોષનો $emf $ અને આંતરિક અવરોધ અનુક્રમે $7\,V$ અને $5\,Ω $ છે.જો ગેલ્વેનોમિટરનો અવરોધ $50\,Ω $ હોય,તો કોષમાંથી નીકળતો પ્રવાહ ................ $A$ હશે.
AIPMT 2013, Medium
a
The a balanced Wheatstone,s birdge
The a balanced Wheatstone,s birdge
For a balanced Wheatstone's bridge
\(\frac{P}{Q}=\frac{R}{S}\)
\(\therefore \quad \frac{10 \,\Omega}{30\, \Omega}=\frac{30\, \Omega}{90\, \Omega}\) or \(\frac{1}{3}=\frac{1}{3}\)
It is a balanced Wheatstone's bridge. Hence no current flows in the galvanometer arm. Hence, resistance \(50\, \Omega\) becomes ineffective.
\(\therefore\) The equivalent resistance of the circuit is
\(R_{\mathrm{eq}}=5\, \Omega+\frac{(10 \,\Omega+30\, \Omega)(30\, \Omega+90\, \Omega)}{(10\, \Omega+30\, \Omega)+(30 \,\Omega+90\, \Omega)} \)
\(=5\, \Omega+\frac{(40\, \Omega)(120\, \Omega)}{40 \,\Omega+120\, \Omega}=5 \,\Omega+30\, \Omega=35\, \Omega\)
Current drawn from the cell is
\(I=\frac{7 \mathrm{V}}{35\, \Omega}=\frac{1}{5} \mathrm{A}=0.2 \,\mathrm{A}\)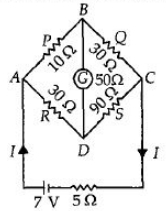
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
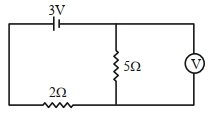
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે, $5\,\Omega$ ના અવરોધ વચ્ચે લગાવેલ વોલ્ટમીટર $2\,V$ નું વાંચન કરે છે. વોલ્ટમીટરનો અવરોધ .......... $\Omega$ છે.View Solution
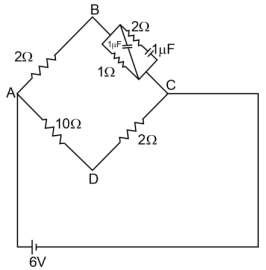
- 2આપેલ પરિપથ. માટે, સ્થાયી સ્થિતિમાં, $\left|V_B-V_D\right|=...........V.$View Solution
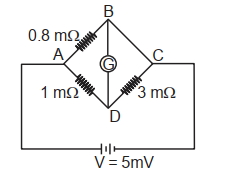
- 3અર્ધવાહક માટે તાપીય અવરોધકતા અંક $\alpha$ માપવા માટે, આકૃતિમાં દર્શાવ્યા અનુસાર વિદ્યુતકીય ગોઠવણ તૈયાર કરવામાં આવે છે. ભૂજા $\mathrm{BC}$ એ અર્ધવાહક ધરાવે છે. આ પ્રયોગ $25^{\circ} \mathrm{C}$ તાપમાને કરવામાં આવે છે અને અર્ધવાહક ધરાવતી ભૂજાનો અવરોધ $3 \mathrm{~m} \Omega$ છે. ભૂજા $\mathrm{BC}$ ને $2^{\circ} \mathrm{C} / \mathrm{s}$ ના અચળ દર થી ઠંડી પાડવામાં આવે છે. જો $10 \mathrm{~s}$ બાદ ગેલ્વેનોમીટર કોણાવર્તન ના દર્શાવતું હોય તો$\alpha$_____________હશે.View Solution
- 4એક પોટેન્શિયોમીટર પરિપથમાં $1.5\, {V}$ નું $EMF$ ધરાવતા કોષ દ્વારા તારની $36\,{cm}$ અંતરે સમતોલન બિંદુ મળે છે.જો પ્રથમ કોષને બદલે $2.5\, {V}$નું $EMF$ ધરાવતો બીજો કોષ બદલવામાં આવે તો તારની કઈ લંબાઈએ સંતુલન બિંદુ મળશે? ($cm$માં)View Solution
- 5View Solutionકોષનો આંતરિક અવરોધ એ કોનો અવરોધ છે?
- 6જ્યારે $2\, mA$ વિદ્યુતપ્રવાહ $1\,s$ માટે પસાર કરવામાં આવે ત્યારે અવરોધમાં વિખેરાતી ઊર્જા $10\, mJ$ છે. અવરોધ $....... \Omega$ છે. (નજીકત્તમ પૂર્ણાકમાં લખો)View Solution
- 7.............. $^oC$ તાપમાને કોપર વાયરનો અવરોધ તેના $0\,^oC$ તાપમાને અવરોધ કરતા $3$ ગણો થશે ? (અવરોધકતાનો તાપમાન ગુણાંક $= 4 = 10^{-3}\, C$)View Solution
- 8View Solutionબદલાતા આડછેદ ધરાવતા ધાતુના વાહકમાંથી સ્થાયી પ્રવાહ વહે છે. તો વાહકની લંબાઈની સાથે કઈ રાશિ અચળ રહે?
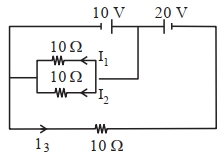
- 9આપેલ પરિપથમાં $\left|\frac{I_1+I_3}{I_2}\right|$ નું મૂલ્ય $x$ મળે છે. $x$ નું મૂલ્ય $......$ થશે.View Solution
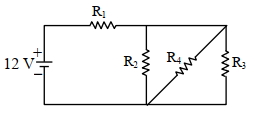
- 10આપેલ આકૃતિમાં, $\mathrm{R}_1=10 \Omega, \mathrm{R}_2=8 \Omega, \mathrm{R}_3=4 \Omega$ અને $\mathrm{R}_4=8 \Omega$ છે. બેટરી આદર્શ અને તેને $12 \mathrm{~V}$ emf છે. પરિપથ માટે સમતુલ્ય અવરોધ અને બેટરી દ્વારા પૂરો પડાતો પ્રવાહ અનુક્મે. . . . . . . . હશે.View Solution