એક વિદ્યાર્થી બસથી $45\, m$ અંતરે પાછળ ઉભો છે.બસ $2.5 \,m/s^2$ ના પ્રવેગ સાથે ગતિ શરૂ કરે છે.વિદ્યાર્થીને બસ પકડવા માટે કેટલા........$m/s$ લઘુત્તમ અચળ વેગથી દોડવું પડે?
Diffcult
c
(c) Let man will catch the bus after \('t'\) sec . So he will cover distance \(ut\).
(c) Let man will catch the bus after \('t'\) sec . So he will cover distance \(ut\).
Similarly distance travelled by the bus will be \(\frac{1}{2}a{t^2}\). For the given condition
\(u\;t = 45 + \frac{1}{2}a\;{t^2}\)\( = 45 + 1.25\;{t^2}\) \([As\;a = 2.5m/{s^2}]\)
\(⇒\) \(u = \frac{{45}}{t} + 1.25\;t\)
To find the minimum value of \(u\)
\(\frac{{du}}{{dt}} = 0\) so we get \(t = 6\sec\) then,
\(u = \frac{{45}}{6} + 1.25 \times 6 = 7.5 + 7.5 = 15\,m/s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઘણા બઘા દડાઓને ઉપર તરફ એકસરખા સમયના અંતરાલમાં ફેંકવામાં આવે છે.એક દડો મહત્તમ ઊંચાઇ પર હોય,ત્યારે બીજા દડાને ફેંકવામાં આવે છે.જો મહત્તમ ઊંચાઇ $5 \,m$ હોય,તો દર મિનિટે ફેંકેલા દડાઓની સંખ્યા કેટલી થાય?($g = 10\,m{s^{ - 2}}$)View Solution
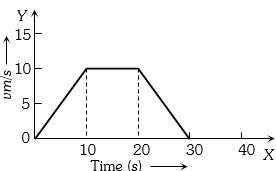
- 2આપેલ ગ્રાફ માટે પદાર્થે કાપેલ અંતર .......... $\mathrm{m}$ હશે.View Solution
- 3એક ટેનિસ બોલને $9.8\,m$ ઉંયાઇએથી ભોંયતળિયા પર મુકત કરવામાં આવે છે. તે જમીન પરથી અથડાઈ પુનઃ $5.0\,m$ ઊંચાઈ પ્રાપ્ત કરે છે. જો બોલ તળિયા સાથે $0.2\,s$ માટે સંપર્કમાં રહે છે. તેની સંપર્ક દરમિયાન સરેરાશ પ્રવેગ $...........ms ^{-2}$ હશે.View Solution
- 4બે ટ્રેન સમાન ટ્રેક પર $40 \,m/s$ ની ઝડપથી એકબીજા તરફ ગતિ કરે છે,જયારે બંને ટ્રેન $2 \,km$ અંતરે હોય,ત્યારે બંને ટ્રેનમાં એકસમાન પ્રતિપ્રવેગ ઉત્પન્ન કરવામાં આવે છે.અથડામણ અટકાવવા માટે પ્રતિ પ્રવેગનું મૂલ્ય કેટલા.........$m/{s^2}$ હોવું જોઈએ?View Solution
- 5એક કાર સ્થિર સ્થિતિમાંથી $\alpha$ જેટલા અચળ દરથી અમુક સમય સુધી પ્રવેગિત ગતિ કરે છે, પછી $\beta$ જેટલા અચળ દરે ધીમી પડીને સ્થિર થાય છે. જો તેના માટેનો કુલ સમય $t$ સેકન્ડ હોય, તો કારે કાપેલ કુલ અંતર કેટલું હશે?View Solution
- 6એક કણનો વેગ $v = kt,$ જયાં $k = 2m/{\sec ^2}$ તો, પ્રથમ $3 \,sec$ માં કેટલા........$m$ અંતર કાપે?View Solution
- 7એક પદાર્થને મુકત કરવામાં આવે છે. $1\, sec$ પછી બીજા પદાર્થને મુકત કરવામાં આવે છે. $3 \,sec$ સમયે બંને પદાર્થ વચ્ચેનું અંતર........$m$ હશે.View Solution
- 8નીચેનામાંથી ક્યો સમય-સ્થાનાંતર આલેપ એ શૂન્ય સાપેક્ષ વેગ સાથે ગતિ કરતાં બે પદાર્થો $P$ અને $Q$ ને રજૂ કરે છે?View Solution
- 9બોલ $A$ ને ઉપરની તરફ $10 \,m / s$ ઝડ૫ સાથે ફેકવામાં આવે છે. એ જ તત્કાલ પર બીજો બોલ $B$ બાકીની ઉંચાઈ $h$ પર થી મુક્ત થાય છે. $t$ સમયે, $A$ ની સાપેક્ષમાં $B$ ની ઝડ૫ કેટલી થાય?View Solution
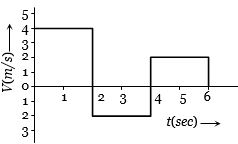
- 10એક પદાર્થનો વેગ વિરુધ્ધ સમયનો આલેખ આપેલ છે.તો પદાર્થે $6\, sec$ માં કરેલ સ્થાનાંતર અને પથલંબાઇ કેટલી હશે?View Solution