એક વર્તુળાકાર તક્તિ $l$ લંબાઈના ઢળતા સમતલ (ઢોળાવ)ની ટોચ ઉપરથી તળિયા સુધી પહોંચે છે. જ્યારે તે સમતલના તળિયે સરકે છે ત્યારે તેન $t$ સેકન્ડનો સમય લાગે છે. જ્યારે તે સમતલના તળિયે ગબડીને પહોંચે છે ત્યારે તે $\left(\frac{\alpha}{2}\right)^{1 / 2} t$ જેટલો સમય લે છે, જ્યાં $\alpha$ .......... હશે.
JEE MAIN 2024, Diffcult
a
For slipping
For slipping
\(\mathrm{a}=\mathrm{g} \sin \theta\)
\(\ell=\frac{1}{2} \mathrm{at}^2 \Rightarrow \mathrm{t}=\sqrt{\frac{2 \ell}{\mathrm{g} \sin \theta}}\)
For rolling
\(\mathrm{a}^{\prime}=\frac{\mathrm{g} \sin \theta}{1+\frac{\mathrm{k}^2}{\mathrm{R}^2}}\left[\mathrm{k}=\frac{\mathrm{R}}{\sqrt{2}}\right]\)
\(\Rightarrow \mathrm{a}^{\prime}=\frac{2 \mathrm{~g} \sin \theta}{3}\)
\(\ell=\frac{1}{2} \mathrm{a}^{\prime}\left(\mathrm{t}^{\prime}\right)^2\)
\(\Rightarrow \mathrm{t}^{\prime}=\sqrt{\frac{6 \ell}{2 \mathrm{~g} \sin \theta}}=\sqrt{\frac{\alpha}{2}} \sqrt{\frac{2 \ell}{\mathrm{s} \sin \theta}}\)
\(\Rightarrow \alpha=3 \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કણ નિયમિત વર્તૂળાકાર ગતિ $L$ જેટલા કોણીય વેગમાનથી કરે છે. જો તેની કોણીય આવૃત્તિ બમણી અને ગતિ ઊર્જા અડધી કરવામાં આવે ત્યારે નવું કોમીય વેગમાન કેટલું થશે ?View Solution
- 2$10\ kg $ દળ અને $ 50\ m $ ની ચક્રાવર્તનની ત્રિજ્યા ધરાવતી તકતી પર $10^5\ [N - m]$ નું બળ યુગ્મ લગાડવામાં આવે છે. કોણીય પ્રવેગની કિંમત $rad/sec^2$ માં કેટલી થશે ?View Solution
- 3બે કણો ના તંત્ર વિશે વિચાર કરો. તેમાં થી એક કણ સ્થિર છે અને બીજો કણ $\vec{f}$ પ્રવેગ ધરાવે છે તો દ્રવ્યમાન કેન્દ્ર નો પ્રવેગ કેટલો થાય?View Solution
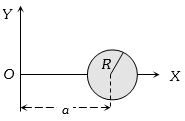
- 4$X-Y$ સમતલમાં આકૃતિ માં દર્શાવ્યા પ્રમાણે $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતી $X$ અક્ષ પર મુકેલી છે $X$ અક્ષ ને અનુલક્ષીને તકતીની જડત્વની ચાકમાત્રા કેટલી થાય $?$View Solution
- 5$20\ g$, $30\ g$ અને $50\ g$ દળના કણનો વેગ અનુક્રમે $10 \vec i,\,10\vec j,\,$ અને $\,10\vec k$ છે. તો આ ત્રણેય કણના દ્રવ્યમાનકેન્દ્રનો વેગ કેટલો થાય ?View Solution
- 6એક ઘર્ષણવાળા ટેબલ પર $a$ બાજુ અને $m$ દળ ધરાવતો સમઘન પડેલો છે . સમઘનની કોઈ એક સપાટી પર ટેબલની સપાટી થી $3a\over 4 $ ઊંચાઈએ લંબરૂપે $ F$ બળ લગાવવામાં આવે છે. તો $F$ ના કેટલા ન્યૂનતમ મૂલ્ય માટે બ્લોક સરક્યાં વગર નમશે ?View Solution
- 7સમાન દળ અને જુદી-જુદી ત્રિજ્યાઓ ધરાવતી બે તક્તિઓ કે જે જુદા-જુદા દ્રવ્યોની બનેલી છે તે એવી રીતે બનાવવામાં આવે છે કે જેથી તેની જાડાઈ અનુક્રમે $1\,cm$ અને $0.5\,cm$ હોય. દ્રવ્યની ઘનતાઓ $3:5$ ના ગુણોતરમાં છે. આ તક્તિઓની તેમનાં વ્યાસને અનુલક્ષીને જડત્વની ચાક્માત્રાઓ $\frac{x}{6}$ નાં ગુણોતરમાં મળે છે. $x$ નું મૂલ્ય $........$ થશે.View Solution
- 8View Solutionમુકત અવકાશમાં એક ઘન ગોળો તેની સંમિતઅક્ષને અનુલક્ષીને ભ્રમણ કરે છે.આ ગોળાની ત્રિજયા તેનું દ્રવ્યમાન સમાન રાખીને વધારવામાં આવે છે.નીચેનામાંથી કઇ ભૌતિકરાશિ આ ગોળા માટે અચળ રહશે?
- 9નળાકાર ટ્યુબમાંથી પસાર થતી દોરીના એક છેડે બિદુવત $z$ દળ $ m $ બાંધેલો છે. આ દોરીને હાથમાં પકડી રાખેલી છે બિંદુવત દળ $2\ m $ ત્રિજ્યાના સમક્ષિતિજ વર્તૂળમાં $4\ m/s$ ની ઝડપની ગતિ કરે છે. ત્યારબાદ દોરીને નીચે ખેચવામાં આવે છે જેથી ત્રિજ્યા ઘટીને $1\ m$ થશે. બિંદુવત દળની નવો રેખીય અને કોણીય વેગ ગણો પ્રારંભિક અને અંતિમ અવસ્થાની ગતિઊર્જાનો ગુણોત્તર ગણો.View Solution
- 10View Solutionઘડિયાળના કલાક-કાંટા અને મિનિટ-કાંટાની કોણીય ઝડપનો ગુણોત્તર .......
