એક વસ્તુ અચળ કાર્યત્વરા (પાવર) ધરાવતા ઉદગમની અસર હેઠળ એક જ દિશામાં ગતિ કેરે છે. તેનું $t$ સમયમાં સ્થાનાંતર. . . . . . . . ના સમપ્રમાણમાં હશે.
JEE MAIN 2024, Diffcult
c
\(\mathrm{P}=\text { costant } \Rightarrow \mathrm{FV}=\text { constant }\)
\(\mathrm{P}=\text { costant } \Rightarrow \mathrm{FV}=\text { constant }\)
\(\Rightarrow \mathrm{m} \frac{\mathrm{dV}}{\mathrm{dt}} \mathrm{V}=\text { constant }\)
\(\int_0^{\mathrm{V}} \mathrm{VdV}=(\mathrm{C}) \int_0^{\mathrm{t}} \mathrm{dt}\)
\(\left(\frac{\mathrm{V}^2}{2}\right)=\mathrm{Ct}\)
\(\mathrm{V} \propto \mathrm{t}^{1 / 2}\)
\(\frac{\mathrm{ds}}{\mathrm{dt}} \propto \mathrm{t}^{1 / 2}\)
\(\int_0^{\mathrm{s}} \mathrm{ds}=\mathrm{K} \int_0^{\mathrm{t}} \mathrm{t}^{1 / 2} \mathrm{dt}\)
\(\mathrm{S}=\mathrm{K} \times \frac{2}{3} \mathrm{t}^{3 / 2}\)
\(\mathrm{~S} \propto \mathrm{t}^{3 / 2}\)
\(\therefore \text { displacement is proportional to }(\mathrm{t})^{3 / 2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
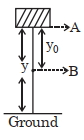
- 1આપેલ આકૃતિમાં ચોસલાં (બ્લોક) ને બિંદુ '$A$' આગળથી મુક્ત કરવામાં આવે છે. ચોસલું જ્યારે બિંદુ '$B$' આગળ પહોંચે ત્યારે ગતિઊર્જાનું સૂત્ર ............... હશે.View Solution
- 2એક સમક્ષિતિજ સમતલ પર $2m$ ત્રિજ્યાવાળી ગોળીય તકતી ગોઠવેલી છે. જેના અંતર્ગોળ પૃષ્ઠ પર $1 g$ દળનો એક કણ દોલીત ગતિ કરે છે. જો કણની ગતિની શરૂઆત સમક્ષિતિજ સમતલથી $1 cm $ ઉંચાઈએ આવેલી તકતી પરના એક બિંદુથી થાય છે અને ઘર્ષણ ગુણાંક $0.01$ છે. કણ સ્થિર સ્થિતિએ રહેલ અંતર્ગોળ પૃષ્ઠના નીચેના ભાગે આવે તે પહેલા તેણે કુલ ........ $m$ અંતર કાપ્યું હશે.View Solution
- 3એક $x$-અક્ષની સાપેક્ષે ગતિમાન પદાર્થ ની સ્થિતિ ઊર્જા $U$ માં તેની સ્થિતિ $(x)$ સાથે થતો ફેરફાર આકૃતિમાં દર્શાવ્યા મુજબ છે. પદાર્થ ક્યાં બિંદુએ સંતુલિત અવસ્થામાં હશે...View Solution
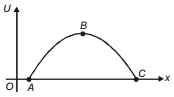
- 4$'m'$ દળ ધરાવતો અને $E$ જેટલી ગતિઊર્જા ધરાવતો બ્લોક (ચિત્રમાં દર્શાવ્યા અનુસાર), જ્યારે તેની ઝડપ અડધી થાય ત્યારે સ્પ્રિંગને $25\;cm$ અંતર સુધી દબાવે છે. વપરાયેલ સ્પ્રિંગ માટે સ્પ્રિંગ અચાળાંક $nE \;Nm ^{-1}$ મળે છે. $n$ નું મૂલ્ય ......... હશે.View Solution
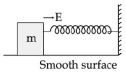
- 5$Y-$ દિશામાં ગતિ કરતા એક પદાર્થ પર $\overrightarrow F = ( - 2\hat i + 15\hat j + 6\hat k)\,N$ બળ લગાવવામાં આવે છે. $Y-$ અક્ષ પર પદાર્થને $10\, m$ ખસેડવા માટે બળ દ્વારા થયેલ કાર્ય ($J$ માં) કેટલું હશે?View Solution
- 6$M$ દળના એક પ્રક્ષેપને એવી રીતે ફેંકવામાં આવે છે તેનો સમક્ષિતિજ વિસ્તાર $4\, km$ થાય. ઉચ્ચત્તમ સ્થાનેથી તેના ફાંટીને બે $M/4$ અને $3M/4$ દળના બે ભાગ થાય છે અને ભારે ભાગ શૂન્ય પ્રારંભિક વેગ થી શિરોલંબ દિશામાં પતન કરે છે. તો હળવા ભાગ નો સમક્ષિતિજ વિસ્તાર(પ્રક્ષેપના પ્રારંભિક સ્થાને થી અંતર) કેટલા ................ $\mathrm{km}$ હશે?View Solution
- 7$M$ અને $2M$ દળ અને $10\, m/s$ અને $5\, m/s$ વેગ ધરાવતા બે કણ ઉગમબિંદુ પાસે સ્થિતિસ્થાપક અથડામણ અનુભવે છે.અથડામણ પછી બંને આકૃતિમાં દર્શાવ્યા મુજબ $v_1$ અને $v_2$ વેગથી ગતિ કરે તો $v_1$ અને $v_2$ અનુક્રમે કેટલા મળે?View Solution
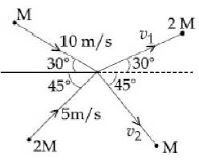
- 8$1 kg $ દળનો કણ $ x$ અક્ષ પર મુક્તપણે ગતિ કરી શકે છે તેની સ્થિતિ ઊર્જા $U(x)\,\, = \,\,\left( {\frac{{{x^2}}}{2}\,\, - \,\,x} \right)$ જૂલ વડે આપવામાં આવે છે. જો કણનું કુલ યાંત્રિક ઊર્જા $2J$ હોય તો કણની મહત્તમ ઝડપ શોધો.View Solution
- 9$1 kg $ દળના એક બોકસને $1m$ લંબાઈના સમક્ષિતિજ સમતલ પર લટકાવેલ છે, જેમાં $8 N$ બળને લીધે શિરોલંબ દિશામાં તેની ઉંચાઈમાં $2m$ નો વધારો થાય છે. તો થતું ચોખ્ખુ કાર્ય કેટલા .....જૂલ હશે ?View Solution
- 10કોઈ વ્યક્તિનું હદય, ધમનીમાં $150\;mm$ જેટલા પારાના દબાણે $5$ લિટર લોહીનું પ્રતિ મિનિટે પમ્પિગ કરે છે. જો પારાની ઘનતા $13.6 \times 10^3\; kg/m^3$ અને $ g=10 \;m/s^2 $ હોય, તો હદયનો પાવર (વોટમાં) કેટલો હશે?View Solution
