એકમ દળવાળો કણ એક પરિમાણમાં એવી રીતે ગતિ કરે છે કે જેથી તેનો વેગ $v(x)= \beta {x^{ - 2n}}$ અનુસાર બદલાય છે. જયાં $\beta $ અને $ n$ અચળાંકો છે, અને $ x $ એ કણનું સ્થાન દર્શાવે છે. $x $ ના વિધેય તરીકે કણનો પ્રવેગ શેના વડે આપવામાં આવે?
AIPMT 2015, Diffcult
Accordind to question, velocity of unit mass varies as
$v(x)=\beta x^{-2 n}..........(i)$
$\frac{d v}{d x}=-2 n \beta x^{-2 n-1}..........(ii)$
Acceleration of the particle is give by
$a=\frac{d v}{d t}=\frac{d v}{d x} \times \frac{d x}{d t}=\frac{d v}{d x} \times v$
Using equation $(i)$ and $(ii),$ we get
$a=\left(-2 n \beta x^{-2 n-1}\right) \times\left(\beta x^{-2 n}\right)=-2 n \beta^2 x^{-4 n-1}$
$v(x)=\beta x^{-2 n}..........(i)$
$\frac{d v}{d x}=-2 n \beta x^{-2 n-1}..........(ii)$
Acceleration of the particle is give by
$a=\frac{d v}{d t}=\frac{d v}{d x} \times \frac{d x}{d t}=\frac{d v}{d x} \times v$
Using equation $(i)$ and $(ii),$ we get
$a=\left(-2 n \beta x^{-2 n-1}\right) \times\left(\beta x^{-2 n}\right)=-2 n \beta^2 x^{-4 n-1}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે કણ $A$ અને $B$ માટે સ્થાનાંતર વિરુદ્ધ સમયનો ગ્રાફ સુરેખ મળે છે જેનો સમયની અક્ષ સાથેનો ખૂણો ${30^o}$ અને ${60^o}$ છે તો તેમના વેગનો ગુણોત્તર ${V_A}:{V_B}$ કેટલો થાય?View Solution
- 2એક કણને $H$ ઊંચાઇના બહુમાળી મકાન પરથી ઊર્ધ્વ દિશામાં $u $ જેટલી ઝડપે ફેંકવામાં આવે છે. કણને જમીન પર પહોંચતા લાગતો સમય તેની મહત્તમ ઊંચાઇએ પહોંચતા લાગતો સમય કરતાં $n$ ગણો છે. $H,u$ અને $n$ વચ્ચેનો સંબંધ શું થાય?View Solution
- 3$t$ થી $(t+1) \mathrm{s}$ સમય અંતરાલમાં, ગતિ કરતા કણ માટે સ્થાનાંતર અને વેગમાં વધારો અનુકમે $125 \mathrm{~m}$ અને $50 \mathrm{~m} / \mathrm{s}$ છે. કણ દ્વારા $(t+2)$ માં સેકન્ડમાં કપાતું અંતર_________$\mathrm{m}$ છે.View Solution
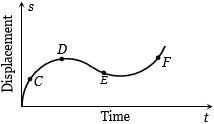
- 4View Solutionગતિ કરતાં કણ માટે સ્થાનાંતર-સમયનો આલેખ આકૃતિમાં દર્શાવ્યો છે.કયાં બિંદુ આગળ કણનો વેગ ૠણ હશે?
- 5View Solutionમુક્ત પતન કરતા એક પદાર્થ ના પ્રથમ,દ્રિતીય,તૃતીય અને ચોથી સેકન્ડમાં કપાયેલ અંતરોનો ગુણોતર ......... હોય છે.
- 6View Solutionવિધાન: અચળ પ્રવેગી ગતિ કરતો પદાર્થ હમેશાં સીધી રેખામાં જ ગતિ કરે છે.
કારણ: અચળ પ્રવેગી ગતિ કરતો પદાર્થ ઝડપ ન પણ વધારે.
- 7$x-$ અક્ષની દિશામાં એક કણને $v_{0}$ જેટલા વેગથી પ્રક્ષિપ્ત કરવામાં આવે છે. કણ પર અવમંદન બળ લાગે છે કે જે ઉદગમથી અંતરનાં વર્ગના સમપ્રમાણમાં, એટલે કે $ma =-\alpha x ^{2}$ છે. અંતર કે જ્યાં કણ અટકશે તે .......View Solution
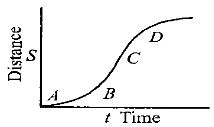
- 8View Solutionકણ માટે અંતર-સમયનો વક્ર આકૃતિમાં બતાવવામાં આવ્યો છે. કણનો મહત્તમ તત્કાલિન વેગ કયા બિંદુની આસપાસ હોય?
- 9$240\;m$ ઊંચા ખડકની ટોચ પરથી બે પથ્થરને અનુક્રમે $10\;ms^{-1}$ અને $40\;ms^{-1}$ ની પ્રારંભિક ઝડપથી ઊર્ધ્વ દિશામાં ફેંકવામાં આવે છે. નીચે દર્શાવેલ આલેખો પૈકી કયો આલેખ બીજા પથ્થરનો પ્રથમ પથ્થરની સખામણીમાં સાપેક્ષ-સ્થાનનો સમય સાથેનો ફેરફાર સૌથી સારી રીતે રજૂ કરે છે?View Solution
(ધારો કે પથ્થરો જમીન પરથી અથડાઇને પાછો ફેંકાતો નથી અને હવાનો અવરોધ અવગણો, $g=10$ $ms^{-2}$ લો.)
(અત્રે આકૃતિઓ ફકત રેખાકૃતિ સૂચવે છે, તેઓ એક જ સ્કેલ પર દોરેલ નથી.)
- 10સીધી રેખાની સાપેક્ષે ગતિ કરી રહેલા પદાર્થ માટે નીચેના આલેખમાંથી કયો એક શક્ય છે? જ્યાં $v$ ઝડ૫, $t$ સમય અને $x$ સ્થાન દર્શાવે છે.View Solution
