એકસમાન ચુંબકીયક્ષેત્રમાં વિદ્યુતભારભારીત કણ અચળ ઝડપ $v$ થી $R$ ત્રિજયાના વર્તુળમાર્ગ પર પરિક્રમણ કરે છે.આ ગતિનો આવર્તકાળ ......
AIPMT 2007,AIPMT 2009, Easy
b
When a particle moves in a magnetic field of intensity B pointing downwards into the page and particle is moving with a speed of \(v\) on the plane of paper:
When a particle moves in a magnetic field of intensity B pointing downwards into the page and particle is moving with a speed of \(v\) on the plane of paper:
\(F = qvB\) (Force of charged particle in a magnetic field)
And we know that
\(F =\frac{ mv ^2}{ r } \quad\) (r is the radius of motion and \(m\) is mass of particle)
\(\Rightarrow qvB =\frac{ mv ^2}{ r }\)
\(\Rightarrow r =\frac{ mv }{ Bq }\)
Now as we know that
\(\omega=\frac{ V }{ r }\)
\(\Rightarrow \omega=\frac{ Bq }{ m }\)
Time period, \(T =\frac{2 \pi}{\omega}\)
\(\Rightarrow T =\frac{2 \pi m }{ Bq }\)
And this shows that it is independent of both radius and velocity.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
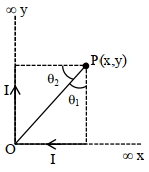
- 1બે અનંત લંબાઈના વિદ્યુતપ્રવાહધારીત તારો છે અને આકૃતિમાં દર્શાવ્યા મુજબ તેમને એવી રીતે ગોઠવવામાં આવે છે કે જેથી તેમના છેડા ઉગમબિંદુ પર રહે. તેમના વિદ્યુતપ્રવાહનો ગુણોત્તર $1: 1$ છે. તો $P$ બિંદુ આગળ ચુંબકીયક્ષેત્ર કેટલુ મળે?View Solution
- 2સમાન ગતિ ઊર્જા ધરાવતા એક પ્રોટોન, એક ડ્યુટેરોન અને એક $\alpha-$ કણ નિયમિત્ત ચુંબકીય ક્ષેત્ર ધરાવતા વિસ્તારમાં ચુંબકીય ક્ષેત્રને લંબ ગતિ કરે છે. તેમના વર્તુળાકાર ગતિપથની ત્રિજ્યાઓનો ગુણોત્તર અનુક્રમે.......હશેView Solution
- 3$25\,\Omega $ અવરોધ ધરાવતા ગેલ્વેનોમીટરના પૂર્ણ આવર્તન માટે $1\,mA$ પ્રવાહની જરૂર પડે છે. $2\,A$ પ્રવાહનું આવર્તન દર્શાવે તેવો એમીટર બનાવવા માટે તેની સાથે કેટલા મૂલ્યનો શંટ અવરોધ જોડાવો પડે?View Solution
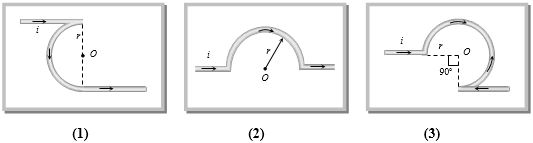
- 4નીચેની આકૃતિમાં $O$ બિંદુ આગળ ચુંબકીયક્ષેત્રનો ગુણોત્તર કેટલો થાય?View Solution
- 5ગેલ્વેનોમીટરનું ગૂંચળું $990\,\Omega$ નો અવરોધ ધરાવે છે. તે $10\,mA$ ના વિધુત પ્રવાહ માટે પૂર્ણ સ્કેલ આવર્તન દર્શાવે છે. તો તેને $1\,A$ ક્ષમતાના એમિટરમાં રૂપાંતર કરવા માટે જરૂરી અવરોધનું મૂલ્ય ............. $\Omega$ ગણો.View Solution
- 6એક પ્રોટોન ચુંબકીય ક્ષેત્રમાં લંબરૂપે વેગ $v$ સાથે દાખલ થાય છે, તો ભ્રમણનો આવર્તકાળ $T$ છે. જો પ્રોટોન $2 v$ વેગ સાથે દાખલ થાય, તો આવર્તકાળ કેટલો હશે?View Solution
- 7$X-Z$ સમતલમાં ઉગમબિંદુ પર એક એક લંબચોરસ ($5\,cm\times 2\,cm$) $100\,$ આંટાવાળા ગુચળામાથી $3\,A$ પ્રવાહ સમઘડી દિશામાં વહે છે.$X$ અક્ષની દિશામાં $1\,T$ ચુંબકીય ક્ષેત્ર પ્રવર્તે છે.જો ગૂચળાંને $Z$ અક્ષ સાથે $45^o$ના ખૂણે વાળવામાં આવે તો તેના પર કેટલા ......$Nm$ ટોર્ક લાગે?View Solution
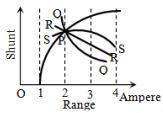
- 8એમીટર શંટ વગર $1$ $A$ ની રેન્જ ધરાવે છે. જુદા જુદા શંટ અવરોધનો ઉપયોગ કરીને એેમીટરની રેન્જમાં ફેરફાર કરી શકાય. તો શંટ અવરોધ અને રેન્જ વચ્ચેનો આલેખ કયો સ્વભાવ ધરાવે છે ?View Solution
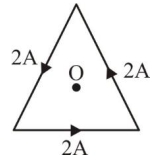
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે $4 \sqrt{3}\,cm$ લંબાઈવાળી સમબાજુ ત્રિકોણની બાજુઓમાં $2\,A$ પ્રવાહ વહે છે, તો ત્રિકોણના કેન્દ્ર $O$ પર ચુંબકીય ક્ષેત્ર $..............$ છે.View Solution
- 10એક લાંબા સોલેનોઈડની એકમ. લંબાઈ દીઠ આાંટાઓની સંખ્યા $10$ છે. તેની સરેરાશ ત્રિજ્યા $5\,cm$ હોય અને તેમાંથી $10\,A$નો વિદ્યુતપ્રવાહ પસાર થતો હોય, તો કેન્દ્ર પાસે મળટી ફલક્સ ઘનતા અને અક્ષ પર છેડા પાસે મળતી ઘનતાનો ગુણોતર કેટલો હશે ?View Solution
