પ્રતિબિંબ વાસ્તવિક અને ઘણું મોટું હોય છે અને વસ્તુ \(C\) અને \(F\) ની વચ્ચે હોવી જોઈએ.
પ્રતિબિંબનો એક છેડો \(A'\) સાથે આપમેળે સમાન મળે છે. તેથી
\({v_A} = \,\,\,{u_{A'}}\,\,\frac{1}{{{v_A}}}\, + \,\,\frac{1}{{{v_A}}}\,\,\, = \,\,\,\frac{1}{{ - {{f}}}}\,\,\,i.e.,\,\,\,{v_A} = \,\,\,{u_A}\,\, = - \,\,\,2{{f}}\)
તેથી સળિયાની લંબાઇ \( = \, \frac{{{f}}}{3}\,\)
\(P\) થી બીજા છેડા \(B\) નું અંતર \({u_B} = \,\,\,2{{f}}\,\, - \,\,\,\frac{{{f}}}{3}\,\, = \,\,\frac{5}{3}\,\,\,{{f}}\)
જો \(P\) થી છેડા \(B\) પ્રતિબિંબ નું અંતર \({v_B}\) હોય તો \(\frac{1}{{{v_B}}}\,\, + \,\,\frac{1}{{ - \frac{5}{3}\,\,{{f}}}}\,\,\, = \,\,\,\frac{1}{{ - {{f}}}}\,\,\,i.e.,\,\,{v_B} = \,\,\, - \frac{5}{2}\,\,{{f}}\)
પ્રતિબિંબ નું કદ \(|{v_B}|\,\, - \,\,|\,\,{v_A}|\,\, = \,\,\,\,\frac{5}{2}\,\,\,{{f}}\,\, - \,\,2{{f}}\,\, = \,\,\frac{1}{2}\,\,{{f}}\,\,\,\)
અને મોટવાણી \(m=\frac{{{v_B} - {v_A}}}{{{u_B} - {u_A}}}=\frac{{\frac{1}{2}\,{{f}}}}{{ - \frac{1}{3}\,\,{{f}}}}= - \frac{3}{2}\)
ઋણ નિશાની દર્શાવે છે કે પ્રતિબિંબ વસ્તુ સાપેક્ષે ઊલટું હોય છે. તેથી વાસ્તવિક હોય છે.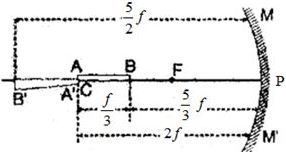
Download our appand get started for free
Similar Questions
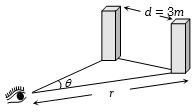
- 1આંખનો વિભેદન પાવર $1\, minute$ છે,$3\, metre$ અંતરે રહેલા બે માણસને કેટલા......$km$ અંતર $r$ સુધી અલગ- અલગ જોઇ શકાય?View Solution
- 2હીરા-હવાની સપાટી પર $630\, {nm}$ તરંગલંબાઇ ધરાવતું લેસર કિરણ $30^{\circ}$ ના ખૂણે આપત કરવામાં આવે છે. તે હીરાથી હવા તરફ ગતિ કરે છે. હીરાનો વક્રીભવનાંક $2.42$ છે અને હવાનો $1$ છે. સાચો વિકલ્પ પસંદ કરો.View Solution
- 3બહિર્ગોળ લેન્સ કાચ ($\mu_g = 1.5$)નો બનેલો છે. જેની હવામાં કેન્દ્રલંબાઈ $4 \,cm$ છે. જો તેની પાણીમાં ($\mu_w = 1.33$) ડૂબાડવામાં આવે તો તેની કેન્દ્રલંબાઈ....... $cm$ થશે?View Solution
- 4$80\,cm$ કેન્દ્રલંબાઇ ધરાવતા બહિર્ગોળ લેન્સ અને $50 \,cm$ કેન્દ્રલંબાઇ ધરાવતા અંતર્ગોળ લેન્સને સંપર્કમાં રાખતા તેનો પરિણામી પાવર કેટલો થાય?View Solution
- 5એક ટાંકી $12.5\,cm$ ઉંચાઈ સુધી પાણીથી ભરેલી છે. ટાંકીને નીચેની સપાટી પર પડેલી સોયની આભાસી ઉડાઈ માઈક્રોસ્કોપ વડે માપવામાં આવતાં $9.4 \,cm$ મળે છે. તો પાણીનો વક્રીભવનાંક ..... હશે.View Solution
- 6એક પેપરને પાણી ભરેલા ગ્લાસની નીચે મૂકવામાં આવે છે. જ્યાં પાણી અને ગ્લાસનો વક્રીભવનાંક અનુક્રમે $1.5$ અને $1.33$ છે. જો ગ્લાસના તળિયાની જાડાઈ $1\, cm$ અને ભરેલા પાણીની ઊંડાઈ $5\, cm$ હોય તો ઉપરથી જોતાં કાગળ કેટલું શીફ્ટ થયેલું દેખાશે?View Solution
- 7મુક્ત અવકાશમાં $3 \,GHz$ આવૃત્તિ ધરાવતું વિદ્યુતચુંબકીય તરંગ $\frac{\lambda}{100}$ પરિમાણ ધરાવતી (જ્યાં $\lambda$ એ મુક્તાવકાશમાં તરંગની તરંગલંબાઈ) વસ્તુની ધાર ઉપર અથડાય છે. ત્યાં બનતી (પ્રકાશની) ધટના શોધો.View Solution
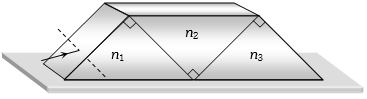
- 8View Solutionઆપેલ આકૃતિમાં કિરણ વિચલન વગર પસાર થતું હોય,તો નીચેનામાથી શું સાચું થાય?
- 9$17.5\, {cm}$ આંતરિક ઊંડાઈ ધરાવતું કાંચની ટ્યુબ ટેબલ પર છે. એક વિદ્યાર્થી તેમાં પાણી $(\mu=4 / 3)$ ભરવાનું શરૂ કરે છે અને તે પાણીની સપાટીને ઉપરથી જુવે છે. જ્યારે તેને એવું લાગે છે કે ટ્યુબ અડધી ભરાય ગઈ છે ત્યારે તે પાણી ભરવાનું બંધ કરે છે. વાસ્તવિકમાં કાંચની ટ્યુબ કેટલી ઊંચાઈ ($cm$ માં) સુધી ભરાઈ હશે?View Solution
- 10સામાન્ય ગોઠવણમાં ગ્રહોનું અવલોકન કરવા માટે નિરીક્ષક દ્વારા ખગોળીય ટેલિસ્કોપનો ઉપયોગ કરવામાં આવે છે. ટેલિસ્કોપના નિર્માણમાં વપરાતા ઓબ્જેક્ટિવ અને આયપીસની કેન્દ્રલંબાઈ અનુક્રમે $20\,m$ અને $2\,cm$ છે. ટેલિસ્કોપ વિશે નીચેના વિધાનો ધ્યાનમાં લોView Solution
$(a)$ ઓબ્જેક્ટિવ અને આયપીસ વચ્ચેનું અંતર $20.02\; m$ છે
$(b)$ ટેલિસ્કોપની મોટવણી $1000$ છે
$(c)$ ગ્રહનું પ્રતિબિંબ સીધું અને નાનું હોય
$(d)$ આયપીસનું છિદ્ર (aperture) ઓબ્જેક્ટિવપીસ કરતાં નાનું છે
સાચા વિધાનો કયા છે?
