ઘન ધાતુના ગોળાની ઘનતા તેનું દળ અને વ્યાસ માપીને કરવામાં આવે છે. ધાતુના ગોળાની ઘનતામાં મહત્તમ ત્રુટિ $\left(\frac{x}{100}\right) \% $ છે. જો દળ અને વ્યાસના માપનમા સાપેક્ષ ત્રુટિ અનુક્રમે $6.0 \%$ અને $1.5 \%$ હોય તો $x$ નું મૂલ્ય કેટલુ હશે?
JEE MAIN 2020, Diffcult
d
\(\rho=\frac{M}{V}=\frac{M}{\frac{4}{3} \pi\left(\frac{D}{2}\right)^{3}}\)
\(\rho=\frac{M}{V}=\frac{M}{\frac{4}{3} \pi\left(\frac{D}{2}\right)^{3}}\)
\(\rho=\frac{6}{\pi} M D ^{-3}\)
taking log
\(\ell n \rho=\ell n \left(\frac{6}{\pi}\right)+\ell n M -3 \ell m D\)
Differentiates
\(\frac{ d p}{\rho}=0+\frac{ d M }{ M }-3 \frac{ d ( D )}{ D }\)
for maximum error
\(100 \times \frac{ d \rho}{\rho}=\frac{ dM }{ M } \times 100+\frac{3 d D }{ D } \times 100\)
\(=6+3 \times 1.5\)
\(=10.5 \%\)
\(=\frac{1050}{100} \%\)
\(x=1050.00\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1દળ $M$, લંબાઇ $L$ ,સમય $T $ અને પ્રવાહ $I $ ના પદમાં વિદ્યુત પરિપથના અવરોધનું પારિમાણિક સૂત્ર શું થાય?View Solution
- 2પ્રયોગમાં સાદા લોલકના દોલનના સમયગાળાની યાદી અનુક્રમે $2.63\,s, 2.56\,s, 2.42\,s, 2.71\,s$ અને $2.80\,s$ છે. તો સરેરાશ નિરપેક્ષ ત્રુટિ કેટલા ........... $s$ હશે?View Solution
- 3સૂચી $-I$ ને સૂચી $- II$ સાથે મેળવો.View Solution
સૂચી $-I$ સૂચી $-II$ $(a)$ $h$ (પ્લાન્કનો અચળાંક) $(i)$ $\left[ M L T ^{-1}\right]$ $(b)$ $E$ (ગતિ ઊર્જા) $(ii)$ $\left[ M L ^{2} T ^{-1}\right]$ $(c)$ $V$ (વિદ્યુત સ્થિતિમાન) $(iii)$ $\left[ M L ^{2} T ^{-2}\right]$ $(d)$ $P$ (રેખીય વેગમાન) $( iv )\left[ M L ^{2} I ^{-1} T ^{-3}\right]$ નીચે આપેલા વિકલ્પોમાંથી સાચા જવાબનું ચયન કરો.
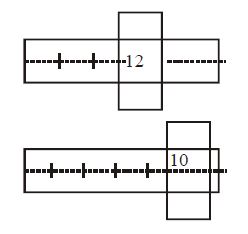
- 4એક સ્ક્રૂ ગેજમાં અમુક ત્રુટિ છે જેનું મૂલ્ય અજ્ઞાત છે. આપની પાસે બે સમાન સળિયા છે. જ્યારે પહેલા સળિયાને સ્ક્રૂ ગેજમાં દાખલ કરવામાં આવે ત્યારે આકૃતિ $(I)$ પ્રમાણે દેખાય છે. જ્યારે બંને સળિયાને સાથે શ્રેણીમાં જોડીને સ્ક્રૂ ગેજમાં દાખલ કરવામાં આવે ત્યારે આકૃતિ $(II)$ પ્રમાણે દેખાય છે. તો સાધનની શૂન્ય ત્રુટિ કેટલા $mm$ હશે?View Solution
$1\,M.S.D. = 100\, C.S.D. = 1\, mm $
- 5$1.5\ mm$ પિચ ધરાવતા સ્ક્રૂગેજની શૂન્ય ત્રુટિ શૂન્ય છે. તેની મુખ્ય સ્કેલમાં $MSD = 1\ mm$ અને વર્તુળાકાર સ્કેલમાં સમાન $100$ કાંપા છે. જ્યારે ગોળાનો વ્યાસ આ સાધન વડે માપવમાં આવે ત્યારે મુખ્ય રેખીય સ્કેલનો $2\ mm$ નો કાંપો દેખાય છે પરંતુ $3\ mm$ નો કાંપો દેખાતો નથી. વર્તુળાકાર સ્કેલનો $76$ મો કાંપો મુખ્ય સકે સાથે બંધ બેસે છે તો ગોળાનો વ્યાસ .......... $mm$ હશે.View Solution
- 6હેનરી દ્વારા લખી શકાય નહી તેવો, ઈન્ડકટન્સનો $SI$ એકમView Solution
- 7$W = \frac{1}{2}\,\,K{x^2}$ સૂત્રમાં $K$ નું પારિમાણિક સૂત્ર શું થાય?View Solution
- 8View Solutionવિદ્યુતસ્થિતિમાનનું પારિમાણિક સૂત્ર શું થાય?
- 9લંબાઈ $l$ અને આડછેદ $a$ વાળા સુવાહકનો વિદ્યુતીય અવરોધ $R$ એ $R = \frac{{\rho l}}{a}$ દ્વારા દર્શાવેલ છે. જ્યાં, $\rho$ એ વિદ્યુતીય અવરોધકતા છે. તો અવરોધકતાને વ્યસ્ત વિદ્યુત વાહકતા $\sigma$ નું પારિમાણિક સૂત્ર શું થાય$?$View Solution
- 10જો એક અવરોધનું મૂલ્ય $10.845 \,\Omega$ હોય અને પસાર થતા વિદ્યુતપ્રવાહનું મૂલ્ય $3.23 \,A$ છે, તો સાર્થક અંકોની સાથે વિજસ્થિતમાનના તફાવત નું મુલ્ય .............. વોલ્ટ થાય ?View Solution
