ગજિયા ચુંબકને ચુંબકીયક્ષેત્રમાં સમતોલન સ્થિતિમાંથી $60^o $ ફેરવવા થતું કાર્ય $\sqrt 3 \;J$ છે. તો તેને આ સ્થિતિમાં રાખવા માટે કેટલા ટોર્ક ($J$ માં) ની જરૂર પડે?
AIPMT 2012, Medium
b
Work done in changing the orientation of a magnetic needle of magnetic moment \(M\) in a magnetic field \(B\) from position \(\theta_{1}\) to \(\theta_{2}\) is given by
Work done in changing the orientation of a magnetic needle of magnetic moment \(M\) in a magnetic field \(B\) from position \(\theta_{1}\) to \(\theta_{2}\) is given by
\(W=M B\left(\cos \theta_{1}-\cos \theta_{2}\right)\)
Here, \(\theta_{1}=0^{\circ}, \theta_{2}=60^{\circ}\)
\(=M B\left(1-\frac{1}{2}\right)=\frac{M B}{2}.........(i)\)
The torque on the needle is
\(\vec{\tau}=\vec{M} \times \vec{B}\)
In magnitude,
\(\tau=M B \sin \theta=M B \sin 60^{\circ}=\frac{\sqrt{3}}{2} M B.........(ii)\)
Dividing \((ii)\) by \((i)\), we get
\(\frac{\tau }{W} = \sqrt 3 \)
\(\tau = \sqrt 3 W = \sqrt 3 \times \sqrt 3 \,{\text{J}} = 3\,{\text{J}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
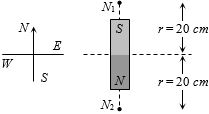
- 1ચુંબકીય મેરીડીયનમાં દક્ષિણ ધુવ ઉત્તર તરફ રહે,તેમ ચુંબક મૂકેલો છે.કેન્દ્રથી $20\,cm $ અંતરે ચુંબકીયક્ષેત્ર શૂન્ય છે.પૃથ્વીનું ચુંબકીયક્ષેત્ર ${B_H} = 0.3 \times {10^{ - 4}},wb/{m^2}$ છે.તો ચુંબકની ચુંબકીય મોમેન્ટ કેટલી થાય?View Solution
- 2એક ટેન્જન્ટ ગેલ્વેનોમીટરની કોઈલનાં આંટાઓની સંખ્યા અને આડછેદનાં ક્ષેત્રફળોની ત્રિજ્યા બમણી કરવામાં આવે તો રિડકશનફેકટર $K$ કેટલો થાય?View Solution
- 3એક સીધી ચુંબકીય પટ્ટીને $44 \mathrm{Am}^2$ જેટલી ચુંબકીય ચાકમાત્રા છે. તે અર્ધવર્તુળાકાર આકારમાં વાળવામાં આવે છે, તો ચુંબકીય પટ્ટીની ચુંબકીય ચાકમાત્રા ............ $\mathrm{Am}^2$ થશે.View Solution
$(\pi=\frac{22}{7}$ લો)
- 4ડિપએંગલ $90^o$ ક્યા હોય?View Solution
- 5ચુંબકીય મેરિડિયનમાં નાનો ગજિયા ચુંબક ધરાવતા દોલન મેગ્નેટોમીટર મૂકવામાં આવે છે. જો પૃથ્વીના $24$ માઇક્રોટેસ્લા સમક્ષિતિજ ચુંબકીય ક્ષેત્રમાં ચુંબક $2$ સેકન્ડના આવર્તકાળથી દોલનો કરે છે. જ્યારે પૃથ્વીનાં ક્ષેત્રની વિરુદ્ધ પ્રવાહધારિત તાર દ્વારા $18$ માઇક્રોટેસ્લાનું સમક્ષિતિજ ક્ષેત્ર ઉત્પન્ન કરવામાં આવે, ત્યારે ચુંબકનો નવો આવર્તકાળ કેટલો થાય?View Solution
- 6એક ગજિયા ચુંબકીય $2.4 \times 10^3\,Am ^{-1}$ ચુંબકીય તીવ્રતા $15\,cm$ લંબાઈ અને $60$ આટાંવાળા સોલેનોઇડ દ્વારા નષ્ટ કરવા (ડીમેગ્નેટાઈઝ) માટે તેમાંથી પસાર કરવો પડતો પ્રવાહ .......$A$.View Solution
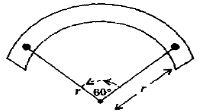
- 7$‘l’ $ લંબાઇનો અને $M$ ચુંબકીય ચાકમાત્રાવાળો એક ગજિયા ચુંબકને આકૃતિમાં દર્શાવ્યા પ્રમાણે ચાપના સ્વરૂપમાં વાળેલું છે. નવી ચુંબકીય ચાકમાત્રા કેટલી થશે?View Solution
- 8View Solutionક્યુરી તાપમાન તે તાપમાન છે જે પછી....
- 9સંપૂર્ણ ડાઈમેગ્નેટિક પદાર્થ નો બનેલો ગોળમાં કેન્દ્ર પર પેરામેગ્નેટિક દ્રવ્ય મૂકેલુ છે. તેને સમાન ચુંબકીયક્ષેત્ર $\overrightarrow{ B }$ માં મૂકવામાં આવે છે. તો પેરામેગ્નેટિક પદાર્થ માં ચુંબકીયક્ષેત્રView Solution

- 10ચુંબક $ 30°$ અને $60°$ ડીપ એન્ગલ ધરાવતા સ્થળે $1$ મિનિટમાં $20 $ અને $ 15$ દોલનો કરે છે.તો તે સ્થળોએ ચુંબકીયક્ષેત્રોનો ગુણોત્તર કેટલો થાય?View Solution
