$H$ ઊંચાઈ પરથી મુકત પતન કરતો એક પદાર્થ, $h$ ઊંચાઈ પર આવેલા એક ઢોળાવ વાળા સમતલ સાથે સંપૂર્ણ સ્થિતિસ્થાપક રીતે અથડાય છે. અથડામણ બાદ પદાર્થનો વેગ સમક્ષિતિજ થાય છે. જો આ પદાર્થ જમીન પર પહોંચવા માટે મહત્તમ સમય લેતો હોય તો $\frac{\mathrm{H}}{\mathrm{h}}$ નું મૂલ્ય .....
JEE MAIN 2024, Diffcult
a
Total time of flight \(=\mathrm{T}\)
Total time of flight \(=\mathrm{T}\)
\(T=\sqrt{\frac{2 h}{g}}+\sqrt{\frac{2(H-h)}{g}}\)
For \(\max\) time \(=\frac{d T}{d h}=0\)
\(\sqrt{\frac{2}{g}}\left(\frac{-1}{2 \sqrt{\mathrm{H}-\mathrm{h}}}+\frac{1}{2 \sqrt{\mathrm{h}}}\right)=0\)
\(\sqrt{\mathrm{H}-\mathrm{h}}=\sqrt{\mathrm{h}}\)
\(\mathrm{h}=\frac{\mathrm{H}}{2} \Rightarrow \frac{\mathrm{H}}{\mathrm{h}}=2\)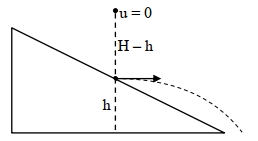
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$3\, meter$ લંબાઈ અને $3\, {kg}$ દળ ધરાવતી સાંકળ ટેબલની ધાર પર લટકે છે જેનો $2\, meter$ જેટલો ભાગ ટેબલ પર છે. જો $k$ એ જ્યારે સાંકળ ટેબલ પરથી સંપૂર્ણ સરકી જાય તે સમયેની જુલમાં ગતિઉર્જા હોય તો ${k}$ નું મૂલ્ય કેટલું હશે? ($\left.g=10\, {m} / {s}^{2}\right)$View Solution
- 2પાણીના ધોધ પરથી, પાણી $100 kg$ પ્રતિ સેકન્ડના દરે ટર્બાઈનની બ્લેડ પર (પડે) વહે છે. જો પાણીના નીચે પડવાની ઉંચાઈ $100 m$ હોય તો, ટર્બાઈનમાંથી ઉત્પન્ન થતો પાવર કેટલો હશે?View Solution
- 3$M$ દળવાળો કણ સ્થિર સ્થિતિમાંથી ગતિની શરૂઆત કરી અચળપ્રવેગી ગતિ કરે છે. જો $T$ સમયમાં કણે પ્રાપ્ત કરેલો વેગ $V$ હોય, તો કણને અપાયેલો પાવર કેટલો હશે?View Solution
- 4$M $ દળનો બ્લોક $ K$ બળ અચળાંક ધરાવતી સ્પિંગ્ર સાથે અથડાવાથી સ્પિંગ્રનું સંકોચન $ L$ થાય છે.તો બ્લોકનું અથડામણ પછીનું મહત્તમ વેગમાન કેટલું થાય?View Solution

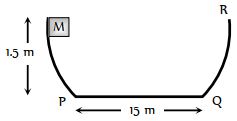
- 5$M $ દળનો પદાર્થ મુકત કરતાં $P$ થી કેટલા ........$m$ અંતરે સ્થિર થશે?પદાર્થ અને સમક્ષિતિજ સપાટી વચ્ચે ઘર્ષણાક $0.2$ છેView Solution
- 6કારને $ F$ અવરોધકબળ લાગતાં $s$ અંતર કાપીને સ્થિર થાય છે.જો કારનું દળ $ 50 \%$ વધે તેા કેટલા.....$s$ અંતરે કાર સ્થિર થશે?View Solution
- 7$x$-અક્ષ પર ગતિ કરી રહેલ એક કણની ( $t)$ સમયે સ્થિતિ $x$ એ $t=\sqrt{x}+2$ સમીકરણ વડે આપેલ છે જ્યાં $x$ મીટરમાં છે અને $t$ સેકન્ડમાં છે. બળ વડે પહેલી ચાર સેકન્ડો માં થયેલ કાર્ય ......... $J$View Solution
- 8$A $ અને $ B$ એમ બે કણો અચળ વેગ અનુક્રમે $\overrightarrow {{v_1}} $ અને $\overrightarrow {{v_2}} $ થી ગતિ કરે છે. પ્રારંભમાં તેના સ્થાન સદિશો અનુક્રમે $\overrightarrow {{r_1}} $ અને $\overrightarrow {{r_2}} $ છે. $A$ અને $B $ ના સંઘાત માટેની શરત શું થાય?View Solution
- 9$e$ રેસ્ટીટયુશન ગુણાંક ધરાવતી સપાટી પર $h$ ઊંચાઇ પરથી દડો મુકત કરતાં બે અથડામણ બાદ દડો કેટલી ઊંચાઈ પ્રાપ્ત કરશે?View Solution
- 10$v$ ઝડપથી ગતિ કરતો ન્યુટ્રોન ધરા અવસ્થામાં રહેલ સ્થિર હાઇડ્રોજન પરમાણુ સાથે સંઘાત કરે છે. તો ન્યૂટ્રોનની ન્યૂનતમ ગતિઉર્જા($eV$ માં) કેટલી હોવી જોઈએ કે જેથી તે અસ્થિતિસ્થાપક સંઘાત અનુભવે?View Solution
