હાઈડ્રોજન પરમાણુ માટે, આકૃત્તિમાં દર્શાવ્યા અનુસાર સંક્રાંતિ $1$ અને $2$ ને આનુષાંગિક તરંગલંબાઈઓ $\lambda_1$ અને $\lambda_2$ છ. $\lambda_1: \lambda_2$ ગુણોત્તર $\frac{x}{32}$ છે. $x$ નું મૂલ્ય $...............$ થશે.
JEE MAIN 2023, Medium
Download our app for free and get started
a
\(\frac{1}{\lambda}= Rz ^2\left[\frac{1}{ n _1^2}-\frac{1}{ n _2^2}\right]\)
\(\frac{1}{\lambda}= Rz ^2\left[\frac{1}{ n _1^2}-\frac{1}{ n _2^2}\right]\)
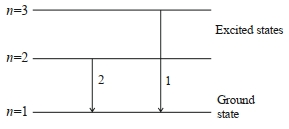
\(\frac{1}{\lambda_1}= Rz ^2\left[\frac{1}{1^2}-\frac{1}{3^2}\right]=\frac{8}{9} Rz ^2\)
\(\frac{1}{\lambda_2}= Rz ^2\left[\frac{1}{1^2}-\frac{1}{2^2}\right]=\frac{3}{4} Rz ^2\)
\(1 / 2 \Rightarrow \frac{\lambda_2}{\lambda_1}=\frac{8}{9} \times \frac{4}{3}=\frac{32}{27}\)
\(\frac{\lambda_1}{\lambda_2}=\frac{27}{32}\)
Ans.\(27\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો $K$ - કવચમાં ઈલેક્ટ્રોનની ઊર્જા $40000 \,eV$ હોય અને કુલીજ ટ્યૂબ આગળ $60000\, eV$ નો સ્થિતિમાન લાગુ પાડવામાં આવે તો નીચેના પૈકી કયા ક્ષ કિરણો આપણને મળશે?View Solution
- 2હાઈડ્રોજનના બોહરના પરમાણીય મોડેલ (પરિકલ્પના)માં, ધારો કે $K,$ $P$ અને $E$ અનુક્રમે ઈલેક્ટ્રોનની ગતીઉર્જા, સ્થિતિઊર્જા અને કુલ ઊર્જા છે. જ્યારે ઈલેકટ્રોન ઉચ્ય સ્તરમાં સંક્રાંતી કરે ત્યારે નીચેનામાંથી સાચો વિકલ્પ પસંદ કરો.View Solution
- 3કાર્બનમાંથી $22\, pm$ તરંગલંબાઈનાં ક્ષ કિરણો આપાત કિરણ પૂંજ સાથે $85^{\circ}$ના ખૂણે પ્રકિર્ણન પામે છે. ક્ષ કિરણો માટે કોમ્પ્ટોન સ્થાનાંતર ......... $pm$ છે ? $\left(\cos 85^{\circ}=0.088\right)$View Solution
- 4હાઈડ્રોજન વર્ણપટ્ટમાં ($ n = 3$ થી $n = 2$ ) પ્રથમ બામર રેખા ની તરંગલંબાઈ $660\,nm ,$ હોય તો બીજી બામર રેખા ( $n =4$ થી $n = 2$ ) ની તરંગલંબાઈ કેટલા ......$nm$ થશે?View Solution
- 5નીચે બે વિધાનો આપેલાં છે.View Solution
વિધાન $I$ : પરમાણુઓ વિધુતીય રીતે તટસ્થ હોય છે, કારણ કે તેમાં સમાન સંખ્યાના ધન અને ઋણ વિધુતભારો હોય છે.
વિધાન $II$ : દરેક તત્ત્વના પરમાણુંઓ સ્થાયી છે અને તેઓ તેમનો લાક્ષણિક વર્ણપટ ઉત્સર્જે છે.
ઉપરોક્ત વિધાનોના સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય ઉત્તર પસંદ કરો.
- 6નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $I$ : હાઈડ્રોજન પરમાણુમાં જ્યારે ઈલેકટ્રોન નીચી ઊર્જા કક્ષા $\left( E _{1}\right)$ માંથી ઉચ્ચ ઊર્જા કક્ષા $\left(E_{2}\right)$ માં કૂદકો (સંક્રાંત) કરે છે ત્યારે ઉત્સર્જાતા વિકિરણની આવૃત્તિ $h f= E _{1}- E _{2}$ વડે આપી શકાય છે.
વિધાન $II$ : ઉચ્ય ઊર્જા કક્ષામાંથી નીચી ઊર્જ કક્ષામાં ઈલેકટ્રોનની સંક્રાંતિ, વિકિરણ આવૃત્તિ $f=\left( E _{2}- E _{1}\right) / h$ સાથે સંકળાયેલ છે.
આ શરતને બોહરની આવૃત્તિ શરત કહે છે.
નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 7View Solutionસ્થિર રહેલા એક હાઇડ્રોજન પરમાણુમાં એક ઇલેકટ્રોન પાંચમી કક્ષામાંથી ધરા-સ્થિતિમાં આવે છે. ફોટોન ઉત્સર્જનના પરિણામે પરમાણુને મળતો વેગ કેટલો હશે?
- 8બ્હોરનાં પરમાણુ મોડલમાં ઇલેક્ટ્રોન અને પ્રોટોન વચ્ચેનું બળ જો $r^4$નાં વ્યસ્ત પ્રમાણમાં હોય તો તંત્રની કુલ ઊર્જા શેનાં પ્રમાણમાં હશે?View Solution
- 9View Solutionક્ષ-કિરણોનું વંકન થતું નથી કારણ કે .....
- 10View Solutionફોટોન .........સાથે સંકળાયેલ છે.