હાઈડ્રોજન પરમાણુમાં $e$ વિદ્યુતભાર અને $m$ દળનો એક ઈલેક્ટ્રોન $r$ ત્રિજ્યાની કક્ષામાં $n$ ભ્રમણ પ્રતિ સેકન્ડ બનાવતો ભમણા કરે છે. જો હાઈડ્રોજનના ન્યુક્લિયસનું દળ $M$ હોય, તો ઈલેક્ટ્રોનની કક્ષીય ગતિ સાથે સંકળાયેલ ચુંબકીય મોમેન્ટ કેટલી છે?
Easy
b
(b)
(b)
Magnetic moment \(= NiA\)
\(i=\frac{q}{T}=e n\)
\(A=\pi r^2\)
\(\text { and } N=1\)
\(\Rightarrow \text { Magnetic moment }(m)=(1)(e n)\left(\pi r^2\right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
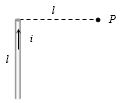
- 1આપેલ આકૃતિ માં $P $ બિંદુએ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 2કોઈ વિસ્તારમાં ચુંબકીય ક્ષેત્ર $\vec{B}=B_0\left(1+\frac{x}{l}\right) \hat{k}$ અસ્તિત્વ ધરાવે છે.$l$ બાજુની અને $i$ વિદ્યુતપ્રવાહ ધરાવતી એક ચોરસ રીંગ તેની બાજુઓ $x-y$ અક્ષને સમાંતર રહે તે રીતે.રીંગ વડે અનુભવતા કુલ ચુંબકીય બળની માત્રા શોધો.View Solution
- 3સાયક્લોટ્રોન દ્વારા આપવામાં આવતો મહત્તમ પ્રવેગિત વિદ્યુતસ્થિતિમાન $12\, {kV}$ હોય, તો સાયક્લોટ્રોનમાં પ્રોટોનને પ્રકાશની ઝડપ કરતાં છઠા ભાગની ઝડપ કરવા તેના પરિભ્રમણની સંખ્યા કેટલી હશે?View Solution
$\left[{m}_{{p}}=1.67 \times 10^{-27} {kg}, {e}=1.6 \times 10^{-19} {C},\right.$ પ્રકાશની ઝડપ $\left.=3 \times 10^{8} {m} / {s}\right]$
- 4આપેલ પરિપથ માટે $O $ બિંદુ પાસે ચુંબકીયક્ષેત્ર આપેલ છે તો નીચે પૈકી કયું સાચું થાય?View Solution
$(i)$ $(ii)$ $(iii)$ (A) $\frac{{{\mu _0}i}}{2r}$ $\odot$ (A) $\frac{{{\mu _0}}}{{2\pi }}\frac{i}{r}(\pi - 2)$ (A) $\frac{{{\mu _0}}}{{2r}}\frac{{2i}}{r}(\pi + 1)$ $\otimes$ (B) $\frac{{{\mu _0}i}}{{2r}}$ $\otimes$ (B) $\frac{{{\mu _0}i}}{{4\pi }}.\frac{i}{r}(\pi + 2)$ $\otimes$ (B) $\frac{{{\mu _0}i}}{{4r}}.\frac{{2i}}{r}(\pi - 1) \otimes $ (C) $\frac{{{3\mu _0}i}}{{8r}}$ $\otimes$ (C) $\frac{{{\mu _0}i}}{4r}$ $\otimes$ (C) $Zero$ (D) $\frac{{{3\mu _0}i}} {{8r}}$ $\odot$ (D) $\frac{{{\mu _0}i}}{4r}$ $\odot$ (D) $Infinite$ 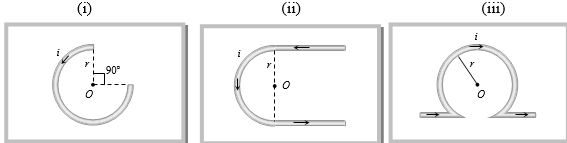
- 5નીચે બે વિધાનો આપેલા છે : એકને ક્થન $(A)$ અને બીજાને કારણ $(R)$ થી દર્શાવેલ છે.View Solution
કથન $(A)$ : સમાંગ ચુંબકીયક્ષેત્રમાં, ગતિમાન વિદ્યુતભારીત કણની ઝડપ અને ઊર્ન સમાન રહે છે.
કારણ $(R)$ : ગતિમાન વિદ્યુભારીત કણ તેની ગતિને લંબ દિશામાં ચુંબકીય બળ અનુભવે છે.
ઉપરોક્ત વિધાનાનોનાં સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો
- 6$N$ આંટા ધરાવતી સ્પાયરલ કોઇલની અંદરની ત્રિજયા $a$ અને બહારની ત્રિજયા $b$ છે. તેમાંથી $I$ પ્રવાહ પસાર કરતાં કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 7View Solutionસમાન લંબાઇના તારમાંથી બનાવેલ વર્તુળ અને ચોરસના કેન્દ્ર પર ચુંબકીયક્ષેત્રનો ગુણોત્તર કેટલો થાય?
- 8ત્રિજ્યા $=0.5\;cm$, પ્રવાહ $=1.5\, A ,$ આંટાઓ $=250,$ પરમીએબીલીટી $=700$ ધરાવતા ટોરોઈડની અક્ષ પર ચુંબકીય ક્ષેત્ર (ટેસ્લા માં) કેટલું હશે?View Solution
- 9આપેલ સ્થાને પૃથ્વીના ચુંબકીય ક્ષેત્રનો સમક્ષિતિજ ઘટક $3.5 \times 10^{-5} \mathrm{~T}$ છે. દક્ષિણ-પૂર્વ થી ઉત્તર-પક્ષિમ દિશામાં $\sqrt{2} \mathrm{~A}$ પ્રવાહ ધરાવતા એક ખૂબ લાંબા સીધા સુવાહકને મૂકવામાં આવે છે. સુવાહક દ્વારા એકમ લંબાઈ દિઢ અનુભવાતું બળ_________$\times 10^{-6} \mathrm{~N} / \mathrm{m}$ છે.View Solution
- 10$2000 $ આંટા અને $1.5 \times 10^{-4}\ m^2$ આડછેદનું ક્ષેત્રફળ ધરાવતો સોલેનોઇડ $2\ A $ પ્રવાહનું વહન કરે છે. સોલેનોઇડને કેન્દ્ર પર અને તેની લંબાઈને લંબ દોરી વડે લટકાવેલ છે કે જેથી તે $5 \times 10^{-2} \;T $ ચુંબકીયક્ષેત્રમાં તેની અક્ષ સાથે $ 30^o$ ના ખૂણે સમક્ષિતિજ સમતલમાં ફરી શકે. સોલેનોઇડ પર લાગતું ટોર્ક કેટલું હશે?View Solution
