હવામાં ગતિ કરતા પ્રકાશ કિરણને ધ્યાનમાં લો ને $\sqrt{2 n}$ વક્રીભવનાંક ધરાવતા માધ્યમ પર આપાત થાય છે. આપાત કોણ વક્રીભૂતકોણ કરતા બમણો છે. તો આપાત કોણ .......... હશે.
JEE MAIN 2022, Diffcult
d
\(i=2 r\)
\(i=2 r\)
\(\sin i \times n_{1}=\sin r \times n_{2}\)
\(\sin i \times 1=\sin \frac{i}{2} \times \sqrt{2 n}\)
\(\frac{\sin i}{\sin \frac{i}{2}}=\sqrt{2 n}\)
\(\frac{\sin \frac{i}{2} \cos \frac{i}{2}}{\sin \frac{i}{2}} \sqrt{2 n}\)
\(\cos \frac{i}{2}=\sqrt{\frac{n}{2}}\)
\(\frac{i}{2}=\cos ^{-1}\left(\sqrt{\frac{n}{2}}\right)\)
\(i=2 \cos ^{-1}\left(\sqrt{\frac{n}{2}}\right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionપોલા કાચના ગોળામાંથી ગોળીય અરીસો બનાવવામાં આવે છે. અરીસાની સામે વસ્તુ મુક્તા પ્ર્તિબિંબ અને મોટવણી
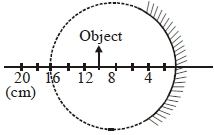
- 2$10cm$ વક્રતાત્રિજયા અને $30cm$ કેન્દ્રલંબાઇ ધરાવતા સમતલ બર્હિગોળ લેન્સનો વક્રીભવનાંક કેટલો થાય?View Solution
- 3બર્હિગોળ લેન્સ દ્વારા વસ્તુનું પ્રતિબિંબ $8 cm$ ઊંચાઇનું મળે છે.હવે લેન્સને બીજા સ્થાને મૂકતાં વસ્તુનું પ્રતિબિંબ $2 cm$ ઊંચાઇનું મળે છે,તો વસ્તુની ઊંચાઇ કેટલા .......$cm$ હશે?View Solution
- 4$h$ ઊંચાઇના માણસને પોતાનું આખું પ્રતિબિંબ જોવા માટે, અરીસાની લઘુત્તમ લંબાઇ કેટલી હોવી જોઈએ?View Solution
- 5$20 \;cm$ અને $25\; cm$ કેન્દ્રલંબાઈ ધરાવતા બે પાતળા બહિર્ગોળ લેન્સને સંપર્કમાં મૂકવામાં આવે તો તેમણે સમતુલ્ય પાવર કેટલો મળે?View Solution
- 6જ્યારે લેન્સથી એક વસ્તુ $u_1$ અને $u_2$ અંતરે હોય, તો સમાન મોટવણીનું અનુક્રમે વાસ્તવિક અને આભાસી પ્રતિબિંબ રચાય છે. લેન્સની કેન્દ્રલંબાઈ કેટલી છે ?View Solution
- 7View Solutionએક નાનો સિકકો પ્રવાહી ભરેલા પાત્રના તળિયે મૂકેલો છે. આ સિકકામાંથી નીકળતું પ્રકાશકિરણ પ્રવાહીની સપાટી સુધી ગતિ કરે છે અને ત્યારબાદ સપાટીને સમાંતર ગતિ કરે છે. આ પ્રવાહીમાં પ્રકાશનો વેગ કેટલો હશે?
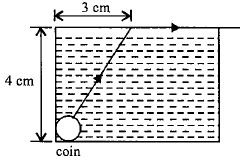
- 8બે લેન્સની કેન્દ્રલંબાઈ $+10\, cm$ અને $-15\, cm$ છે. ત્યારે તેમને એકબીજાને સંપર્કમાં રાખતાં બહિર્ગોળ લેન્સ તરીકે વર્તેં છે. તેનું વર્ણ વિપથન શૂન્ય છે તો વિભાજન પાવરનો ગુણોત્તર .......છે.View Solution
- 9$60^o $ નો પ્રિઝમકોણ ધરાવતા પ્રિઝમ માટે લઘુત્તમ વિચલનકોણ $30^o$ હોય,તો આપાતકોણ કેટલા .....$^o$ હશે?View Solution
- 10View Solutionગુરુધ્ષ્ટિ નિવારવા માટે કયા લેન્સ પહેરવા પડે?
