$I$ પ્રવાહ ધરાવતી એક વર્તુળાકાર લૂપની દ્વિદ્યુવી ચાકમાત્રા $m$ છે.અને લૂપના કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર $B_1$ જેટલું છે.જયારે પ્રવાહ અચળ રાખીને દ્વિદ્યુવી ચાકમાત્રા બમણી કરવામાં આવે છે,ત્યારે લૂપના કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર $B_2$ થાય છે. $\frac{{{B_1}}}{{{B_2}}}$ ગુણોત્તર ______.
JEE MAIN 2018, Medium
b
Magnetic field at the centre of \(\operatorname{loop}, B_{1}=\frac{\mu_{0} I}{2 R}\)
Magnetic field at the centre of \(\operatorname{loop}, B_{1}=\frac{\mu_{0} I}{2 R}\)
Dipole moment of circular loop is \(m=I A\)
\(\mathrm{m}_{1}=\mathrm{I} \cdot \mathrm{A}=\mathrm{I} \pi \mathrm{R}^{2} \quad\{\mathrm{R}=\text { Radius of the loop }\}\)
If moment is doubled (keeping current constant) \(R\) becomes \(\sqrt{2 \mathrm{R}}\)
\({{\text{m}}_2} = {\text{L}}\pi {(\sqrt 2 {\text{R}})^2} = 2.{\text{I}}\pi {{\text{R}}^2} = 2{{\text{m}}_1}\)
\(B_{2}=\frac{\mu_{0} I}{2(\sqrt{2} R)}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$40\, cm$ લંબાઇ ધરાવતા તારમાંથી $3\,A $ પ્રવાહ પસાર કરીને $500$ ગોસ ચુંબકીયક્ષેત્ર સાથે $ 30^\circ $ ના ખૂણે મૂકતાં તેના પર કેટલું બળ લાગે?View Solution
- 2$50\, keV$ ની ગતિઊર્જા ધરાવતો ડયુટેરોન $\overrightarrow B$ ચુંબકીયક્ષેત્રને લંબ સમતલમાં $0.5\;m$ ત્રિજ્યાની વર્તુળાકાર કક્ષામાં ગતિ કરે છે. સમાન સમતલમાં સમાન $\overrightarrow B$ ચુંબકીયક્ષેત્રમાં $0.5\;m$ ત્રિજ્યાની વર્તુળાકાર કક્ષામાં પ્રોટોનની ગતિઊર્જા ......$keV$ થાય?View Solution
- 3$G$ જેટલો અવરોધ અને $S$ જેટલો શંટ જોડી રૂપાંતરીત કરેલા ગેલ્વેનોમીટરમાં વાસ્તવમાં થતા કોણાવર્તનો $n$ છે. જ્યારે તેનો ગુણવત્તા અંક (figure of merit) $K$ હોય તો કુલ પ્રવાહ $I$....... થશે.View Solution
- 4એક શિક્ષક દ્વારા અર્ધ કોણાવર્તન રીતની મદદ્થી ગેલ્વેનોમીટરનો આંતરિક અવરોધ $(G)$ માપવાનો પ્રયોગ, ભૌતિક શાસ્ત્રની લેબોરેટરીરીમાં ફાળવવામાં આવે છે. વિદ્યાર્થીઓ ગેલ્વેનોમીટરમાં અર્ધ કોણાવર્તન અને $\frac{1}{3}$ આવર્તન બંને અવલોકનો લે છે. તેઓ તેમના શિક્ષકને પૂછે છે કે શું $\frac{1}{3}$ આવર્તન રીતનો ઉપયોગ $G$ નું મૂલ્ય માપવા માટે કરી શકાય કે નહી, નીચેનામાંથી ક્યો સાચો પ્ર્ત્યુતર હશે$?$View Solution
- 5ઇલેક્ટ્રોન ઘન $+x$ દિશામાં $6 \times 10^{6}\, ms ^{-1}$ ના વીગથી ગતિ કરે છે. વિધુતક્ષેત્ર $+ y$ દિશામાં $300 \,V / cm$ છે. ઇલેક્ટ્રોન $+ x-$ દિશામાં ગતિ કરે તે માટે ચુંબકીયક્ષેત્રનું મૂલ્ય અને દિશાView Solution
- 6$L$ બાજુવાળી સમક્ષિતિજ ચોરસ લૂપમાં $i$ પ્રવાહ પસાર થાય છે.હવે અડધી લૂપને વાળીને શિરોલંબ કરવામાં આવે છે. $ \overrightarrow {{\mu _1}} $ અને $ \overrightarrow {{\mu _2}} $ એ વાળ્યા પહેલા અને પછીની ચુંબકીય મોમેન્ટ હોય,તો નીચેનામાથી શું સાચું થાય?View Solution
- 7વીજપ્રવાહ ધારિત લંબ ચોરસ લૂપ $PQRS$ સમાન તારની બનેલી છે. $P R=Q S=5\,cm$ અને $P Q=R S=100\,cm$ છે. જો એમિટર પ્રવાહનું અવલોકન $I$ થી $2I$ બદલાય તો તાર $PQ$ પર તાર $RS$ ને લીધે લાગુ પડતા પ્રતિ લંબાઈ ચુંબકીયબળનો ગુણોત્તર $\left(f_{P Q}^I: f_{P Q}^{2 I}\right)$ $................$ થાય.View Solution
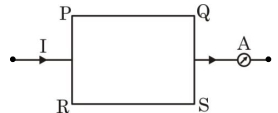
- 8તારમાં $ i $ પ્રવાહ ઘન $X-$ દિશામા પસાર થાય છે.ચુંબકીયક્ષેત્ર $\overrightarrow B = {B_0}$ ($\hat i + \hat j + \hat k)$ $T$ છે.તો તેના પર કેટલું બળ લાગશે?View Solution
- 9જ્યારે બે ગુંચળામાંથી સમાન વિદ્યુત પ્રવાહ પસાર થાય છે. ત્યારે તેના કેન્દ્ર પાસે સમાન ચુંબકીય ક્ષેત્ર ઉત્પન્ન થાય છે. જો ગૂંચળાઓમાં આંટાઓની સંખ્યાનો ગુણોતર $8 : 15$ હોય,તો તેની ત્રિજ્યાનો ગુણોત્તર કેટલો હશે ?View Solution
- 10$100\,\Omega $ અવરોધ ધરાવતા ગેલ્વેનોમીટર પર $50\,$ કાપા છે જેની પ્રવાહ સંવેદિતા $20\,\mu A / $કાપો છે. જેને $0-2\, V$, $0-10\, V$ અને $0-20\, V$ એમ ત્રણ રેન્જના વૉલ્ટ માપી શકે તેવા વોલ્ટમીટરમાં ફેરવવા માટે નીચેનામાથી ક્યો પરિપથ વાપરવો જોઈએ?View Solution
