In a right triangle $ABC,$ right-angled at $B, D$ is a point on hypotenuse such that $\text{BD}\perp\text{AC}.$ If $\text{DP}\perp\text{AB}$ and $\text{DQ}\perp\text{BC}$ then prove that.
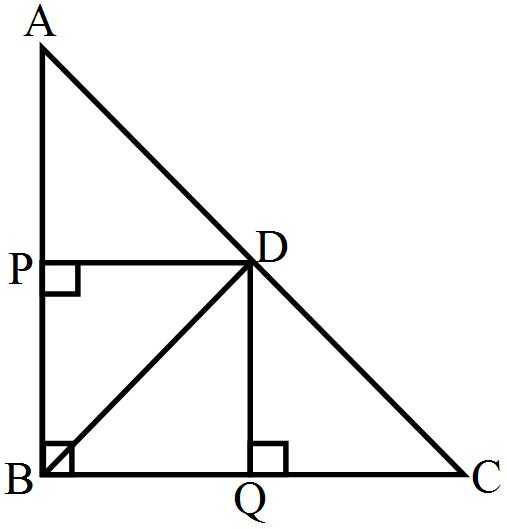
- $\text{DQ}^2=\text{DP}.\text{DQ}$
- $\text{DP}^2=\text{DQ}.\text{AP}$

We know that
when a perpendicular is drawn from the vertex of a triangle on to the hypotenuse, then the triangles on both sides of the perpendicular are similar to eachother and the to the whole triangle.
$\Rightarrow\frac{\text{DQ}}{\text{DQ}}=\frac{\text{QB}}{\text{QC}}$
$\Rightarrow\text{DQ}^2=\text{QB}.\text{QC}$
Since all the angles of PBQD are $90^\circ ,$
$PBQD$ is a rectangle.
$\Rightarrow QB = DP$ and $PB = DQ ....(i)$
$\Rightarrow DQ^2 = DP . QC$
$\Rightarrow\frac{\text{DP}}{\text{PB}}=\frac{\text{AP}}{\text{DP}}$
$\Rightarrow\frac{\text{DP}}{\text{DQ}}=\frac{\text{AP}}{\text{DP}}\dots(\text{using }(\text{i}))$
$\Rightarrow\text{DP}^2=\text{DQ}.\text{AP}$
when a perpendicular is drawn from the vertex of a triangle on to the hypotenuse, then the triangles on both sides of the perpendicular are similar to eachother and the to the whole triangle.
- In $\triangle\text{DBC},$
$\Rightarrow\frac{\text{DQ}}{\text{DQ}}=\frac{\text{QB}}{\text{QC}}$
$\Rightarrow\text{DQ}^2=\text{QB}.\text{QC}$
Since all the angles of PBQD are $90^\circ ,$
$PBQD$ is a rectangle.
$\Rightarrow QB = DP$ and $PB = DQ ....(i)$
$\Rightarrow DQ^2 = DP . QC$
- Similarly, since $PD$ is a perpendicular on $AB$,
$\Rightarrow\frac{\text{DP}}{\text{PB}}=\frac{\text{AP}}{\text{DP}}$
$\Rightarrow\frac{\text{DP}}{\text{DQ}}=\frac{\text{AP}}{\text{DP}}\dots(\text{using }(\text{i}))$
$\Rightarrow\text{DP}^2=\text{DQ}.\text{AP}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
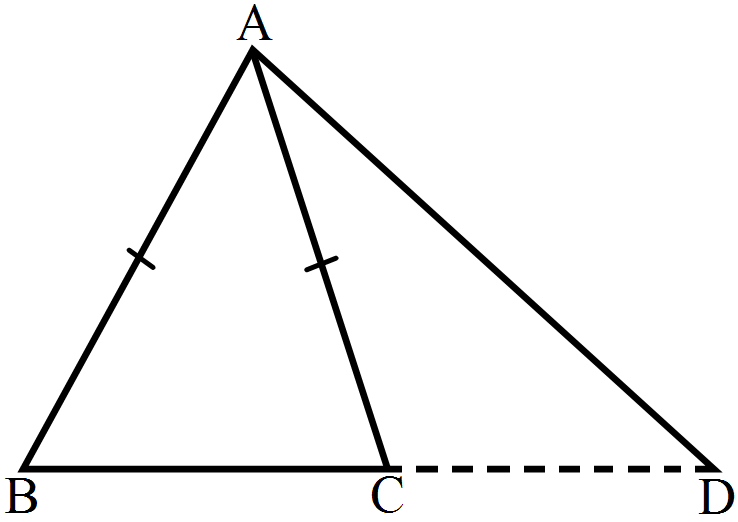
- 1In $\triangle\text{ABC},\text{AB}=\text{AC}.$ Side BC is produced to D. prove thatView Solution
$(\text{AD}^2-\text{AC}^2)=\text{BD}.\text{CD}$
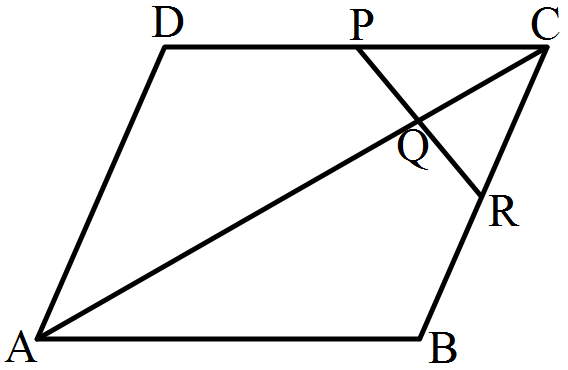
- 2ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that $\text{CQ}=\frac{1}{4}\text{AC}.$ If PQ produced meets BC at R, prove that R is the midpoint of BC.View Solution
- 3The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the rerimeter of $\triangle\text{DEF}$ is 25cm, find the perimeter of $\triangle\text{ABC}.$View Solution
- 4In a $\triangle\text{ABC},\text{AD}$ is the bisector of $\angle\text{A}.$ If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.View Solution
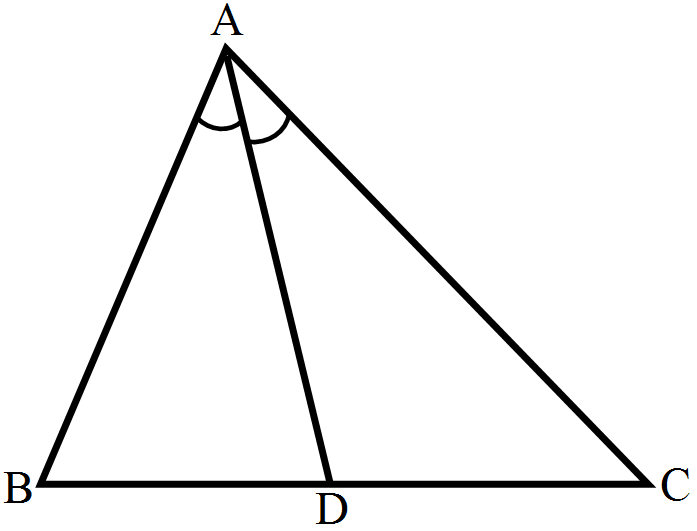
- 5In $\triangle\text{ABC},$ the bisector of $\angle\text{B}$ meets AC at D. A line PQ || AC meets AB, BC and BD at P, Q and R respectively.View Solution
Show that PR × BQ = QR × BP.
- 6View SolutionState the two properties which are necessary for given two triangles to be similar.
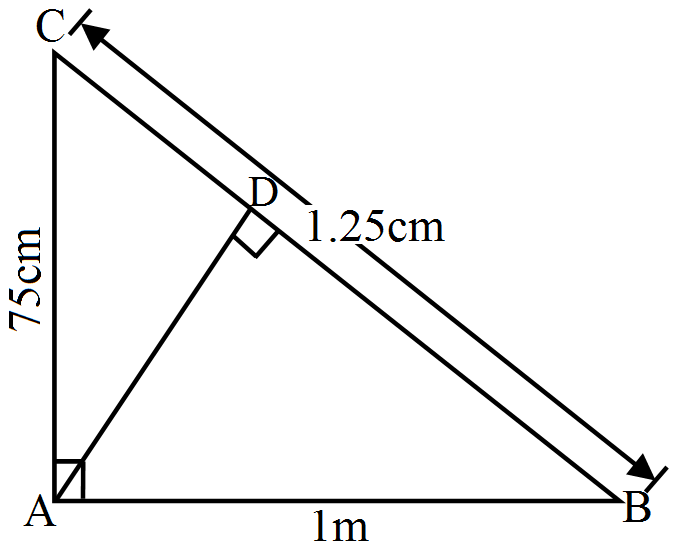
- 7In the given figure, $\angle\text{CAB}=90^\circ$ and $\text{AD}\perp\text{BC}.$ Show that $\triangle\text{BDA}\sim\triangle\text{BAC}.$ If AC = 75cm, AB = 1m, and BC = 1,25m find AD.View Solution
- 8View SolutionThe sides of certain triangles are given below. Determine them are right triangles:
1.6cm, 3.8cm, 4cm. - 9In a trapezium ABCD, it is given that AB || CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that $\text{ar}(\triangle\text{AOB})=84\text{cm}^2.$ Find $\text{ar}(\triangle\text{COD}).$View Solution
- 10View SolutionThe sides of certain triangles are given below. Determine them are right triangles:
9cm, 16cm, 18cm.
