ધારો કે \(t\) એ ઈન્ડસ વેલી સભ્યતાનું આયુષ્ય છે.
ક્ષયનો દર એટલે કે \(R\) એ \(R \propto N\) અથવા \(R ={ \lambda }N\)
\(N = N_0e^{-\lambda t} \, ,R = {\lambda} N 0e^{-\lambda t}= R_0e^{-\lambda t}\) જ્યાં \(R_0 = {\lambda} N_0\) પ્રારંભિક ક્ષય દર
આથી \(\,\frac{{{R_0}}}{R}\,\, = \,\,{e^{ - \lambda t}}\,\,.....\,\,(i)\,\,\)
તેથી \(\frac{R}{{{R_0}}}\, = \,\,\frac{9}{{15}}\, = \,\,\frac{3}{5}\,\,\,......\,\,(ii)\)
સમી \((I)\) અને \((II)\) પરથી, \(e^{-\lambda t} = 3/5 ⇒ e^{\lambda t} = 5/3\)
\( \Rightarrow \,\,\,\,\lambda t\,\, = \,\,\ln \,\,(5/3)\,\,\,\,\, \Rightarrow \,\,\,\,t\,\, = \,\,\frac{{\ln \,(5/3)}}{\lambda }\,\,\,\,\,\)
\( \Rightarrow \,\,\,\,t\,\, = \,\,\frac{{\ln \,\,(5/3)}}{{\ln 2}}\,\, \times \,\,{T_{1/2}}\)
\(=\,\,\frac{{\log \,\,(5/3)}}{{\log 2}}\,\, \times \,\,5730\,\,y\,\,\,\,\left( {as\,\,{T_{1/2}} = \,\,\frac{{\ln \,2}}{\lambda }} \right)\)
\(\therefore\) \(t\,\, = \,\,\frac{{0.2219}}{{0.3010}}\,\, \times \,\,5730\,\,y\,\, = \,\,4224\,\,year\)
Download our appand get started for free
Similar Questions
- 1રેડિયો એક્ટિવ પદાર્થનું અર્ધ આયુષ્ય $100$ સે છે. $5$ મિનિટ બાદ $8$ ગ્રામ પદાર્થમાં કેટલા ........... ગ્રામ ઉત્તેજીત પદાર્થ બાકી હશે?View Solution
- 2રેડિયોએકિટવ તત્ત્વ માટે વિભંજન દર $ \left( {\frac{{dN}}{{dt}}} \right) $ વિરુધ્ધ સમય $(t)$ નો ગ્રાફ કેવો મળે?View Solution
- 3$15$ કલાકમાં રેડિયો એક્ટિવ પદાર્થ ઉત્તેજીત જથ્થામાં તેના પ્રારંભિક મૂલ્યથી $1/64$ જેટલો ઘટાડો થાય છે. તેનું અર્ધ આયુષ્ય ....... કલાક શોધો.View Solution
- 4રેડિયો-ઍક્ટિવ $Po$(પોલોનિયમ)નો અર્ધઆયુ $138.6\, day$ છે, તો દસ લાખ પોલોનિયમ પરમાણુઓ માટે $24\, hour$ માં વિભંજનની સંખ્યા ........View Solution
- 5${}^{66}Cu$ નું રૂપાંતર $Zn$ માં $15\, minutes$ માં $\frac{7}{8}$ નું વિભાજન થાય છે. તો તેનો અર્ધઆયુ ........ મિનિટView Solution
- 6$ ^{66}Cu $ નો $ \frac{7}{8} $ મો ભાગ વિભંજન થતાં $15$ મિનિટ લાગે છે,તો અર્ધઆયુ સમય કેટલા ........$min$ હશે?View Solution
- 7View Solutionરેડિયમની વિશિષ્ટ એક્ટિવીટી ........ની નજીક છે.
- 8View Solutionસૌર ઊર્જાનું મુખ્ય કારણ શું છે?
- 9ન્યુક્લિયોનદીઠ બંધન-ઊર્જા $(BE/A)$ વિરુદ્ધ પરમાણુદળાંક $(A)$ નો આલેખ આકૃતિમાં દર્શાવેલ છે. તો કયો વિકલ્પ સાચો થાય?View Solution
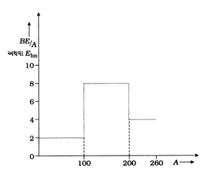
- 10ન્યુકિલયર સંલયન પ્રક્રિયામાં બે $m_1$ અને $m_2$ દળના ન્યુકિલયસ ભેગા થઇને $m_3$ દળનું ન્યુકિલયસ બનાવે છે.તો...View Solution
