જલીય દ્રાવણમાં ક્લોરિનની ઓક્સિડેશનકર્તા તરીકેની ક્ષમતા નીચેના માપદંડો પરથી નક્કી થાય છે.
$\frac{1}{2}C{l_2}(g)\xrightarrow{{\frac{1}{2}{\Delta _{diss}}{H^\Theta }}}Cl(g)\xrightarrow{{{\Delta _{eg}}{H^\Theta }}}$ $C{l^ - }(g)\xrightarrow{{{\Delta _{Hyd}}{H^\Theta }}}C{l^ - }(aq)$
તો $\frac{1}{2}C{l_2}(g)$ ના $Cl^-_{(aq)}$ માં રૂપાંતમાં ઊર્જાનો ફેરફાર ............. $\mathrm{kJ\,mol}^{-1}$ જણાવો.
$({{\Delta _{diss}}H_{C{l_2}}^\Theta } = 240\,kJ\,mol^{-1}, {{\Delta _{eg}}H_{C{l}}^\Theta }= -349 \,kJ\,mol^{-1},$${{\Delta _{Hyd}}H_{C{l}}^\Theta }= -381 \,kJ\,mol^{-1})$
AIEEE 2008, Medium
Download our app for free and get started
b
The energy involved in the conversion of
The energy involved in the conversion of
\(\frac{1}{2} C_{2}(g)\) to \(C l^{-1}(a q)\) is given by
\(\Delta H=\frac{1}{2} \Delta_{d i s s} H_{C l_{2}}^{(-)}+\Delta_{e g} H_{C l}^{(-)}+\Delta_{h y l} H_{C l}^{(-)}\)
Substituting various values from given data, we get
\(\Delta H=\left(\frac{1}{2} \times 240\right)+(-349)+(-381)\, k J \,m o l^{-1}\)
\(=(120-349-381)\, k J\, m o l^{-1}\)
\(=-610 \,k J \,m o l^{-1}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$CO ({-1}10 \,KJ\, mol^{-1}$) અને $CO_2(-394 \,KJ$ મોલ$^{-1}$) ના નિર્માણની પ્રમાણિત એન્થાલ્પી છે. જ્યારે $1$ મોલ ગ્રેફાઈટ સળગે ત્યારે દહન ઉષ્મા કેટલા ............... $\mathrm{KJ}$ થશે ?View Solution
- 2View Solutionનીચેના પૈકી ક્યુ સાચું છે ?
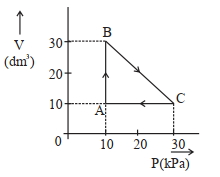
- 3$Image$ એક આદર્શ વાયુ બિંદુ $A$ થી શરૂઆત કરીને ચક્રિય સ્થાનાંતર કરે છે અને ઉપરની આકૃતિમાં દર્શાવ્યા પ્રમાણે દોરેલા પથ $\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C} \rightarrow \mathrm{A}$ દૃવારા તે જ બિંદુ પર પાછો ફરે છે. આ પ્રક્રમમાં થયેલ કુલ કાર્ય ____________$\mathrm{J}$ છે.View Solution
- 4$C + O_2 \rightarrow CO_2$ પ્રક્રિયા માટે એન્થાલ્પી ...... હોય છે.View Solution
- 5નીચેના પ્રકમો પરથી પ્રકિયા $B + D \rightarrow E + 2C$ માટે $\Delta H$ નું મૂલ્ય કેટલા ........... $\mathrm{kJ/mol}$ હશે તે જણાવો.View Solution
$\Delta H \,(kJ/mol)$ $\frac 12 A \rightarrow B$ $+150$ $3B \rightarrow 2C + D$ $-125$ $E + A \rightarrow 2D$ $+350$ - 6View Solutionનીચેનામાંથી કઈ ઉષ્માશોષક પ્રક્રિયા સ્વયંભૂ છે
- 7$C_{(s)} + O_{2(g)} \rightarrow CO_{2(g)}$ માટે ......View Solution
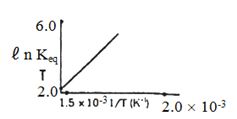
- 8પ્રક્રિયા માટે $ℓ\,n\, K_{eq}$ વિરૂદ્ધ તાપમાનનો આલેખ દોરવામાં આવે તો પ્રક્રિયા...... હોવી જોઈએ.View Solution
- 9જો કોઈ પદાર્થ માટે ગલનબિંદુ $T_B$ તથા ઠારબિંદુ $T_A$ હોય તો એન્ટ્રોપીમાં થતા ફેરફાર અને તાપમાન વચ્ચેનો સાચો સંબંધ કયા આલેખ વડે દર્શાવી શકાય ?View Solution
- 10$K_c$ $P + Q $ $\rightleftharpoons$ $ R + C$ એ $10^{-2}$ છે અને $K_f $ $=$ $10^{-1}$ છે તો પ્રતિગામી સક્રિય માટે દર અચળાંક ....... થશે.View Solution