જમીન પર રાખેલ ટાંકીમાં $10\,m$ ઊંચાઈ સુધી પાણી ભરેલ છે.તેમાં બે જમીનથી $3\, m$ અને $7\, m$ ઊંચાઈ કાણાં પડેલા છે.તો બહાર આવતા પાણી માટે શું કહી શકાય?
AIIMS 2014, Diffcult
a
Velocity of water from hole
Velocity of water from hole
\(A = {v_1} = \sqrt {2gh} \)
Velocity of water from hole \(B\)
\( = {v_2} = \sqrt {2g\left( {{H_0} - h} \right)} \)
Time of reching the ground from hole \(B\)
\( = {t_1} = \sqrt {2\left( {{H_0} - h} \right)/g} \)
Time of reaching the ground from hole \(A\)
\( = {t_2} = \sqrt {2h/g} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જ્યારે બ્લોક હવામાં હોય ત્યારે સ્પ્રિંગ માપન $60 \,N$ છે. જ્યારે તેને પાણીની અંદર નાખવામાં આવે ત્યારે તેનું માપન $40 \,N$ છે. તો બ્લોકનું વિશિષ્ટ ઘનતા કેટલું ?View Solution
- 2$P$ દબાણનો તફાવત ધરાવતી નળીમાં પ્રવાહીનું વહન થાય છે. જો બમણી ત્રિજયા અને બમણી લંબાઇ ધરાવતી નળીમાં બમણા દરથી પ્રવાહીનું વહન કરવા માટે જરૂરી દબાણનો તફાવત કેટલો થાય?View Solution
- 3તમે એક ઓલિક ઍસિડનું મંદ દ્રાવણ લીધું છે કે જેમાં પ્રતિ $cm ^{3}$ દ્રાવણમાં ઓલિક ઍસિડનું પ્રમાણ $0.01 \,cm ^{3}$ છે. $\left(\frac{3}{40 \pi}\right)^{\frac{1}{3}} \times 10^{-3}\; cm$ ત્રિજ્યાના દ્રાવણના $100$ ટીપાંથી $4\;cm ^{2}$ ક્ષેત્રફળ ધરાવતું પાતળું સ્તર બનાવવામાં આવે છે. તેમાં ઓલિક એસિડની જાડાઈ $x \times 10^{-14} \;m$ છે. જ્યાં $x$ કેટલું હશે?View Solution
- 4કોલમ - $\mathrm{I}$ માં બળ અને કોલમ - $\mathrm{II}$ માં તેનો ઉપયોગ આપેલો છે, તો તેમને યોગ્ય રીતે જોડો :View Solution
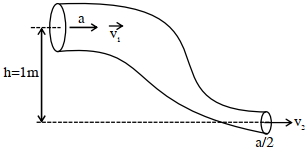
કોલમ - $\mathrm{I}$ કોલમ - $\mathrm{II}$ $(a)$ સંસક્તિ બળ $(i)$ ચૉક વડે કાળા પાટિયા પર લખવામાં ઉપયોગી. $(b)$ આસક્તિ બળ $(ii)$ સોલ્ડરિંગ કરવામાં ઉપયોગી $(iii)$ પ્રવાહીને ગોળાકાર ટીપાં બાનવવામાં ઉપયોગી - 5$800 \,kgm ^{-3}$ ઘનતા ઘરાવતું એક આદર્શ પ્રવાહી (આકૃતિમાં દર્શાવ્યા મુજબ) એક વળેલી નળીમાંથી સહેલાઈથી/સરળતાથી વહન પામે છે.આ નળીનો આડછેદ $a$ થી ઘટીને $\frac{a}{2}$ થાય છે. પહોળા અને સાંકળા છેડાઓ વચ્ચે દબાણનો તફાવત $4100 \,Pa$ છે. પહોળા છેડા આગળ પ્રવાહીનો વેગ $\frac{\sqrt{x}}{6} ms ^{-1}$ છે. $x$ નું મૂલ્ય ........ થશે. $\left( g =10 ms ^{-2}\right.$ છે.)View Solution
- 6કોલમ - $\mathrm{I}$ માં જુદી જુદી રાશિઓ અને કોલમ - $\mathrm{II}$ માં તેમના પારિમાણિક સૂત્ર લખેલાં છે, તો તેમને યોગ્ય રીતે જોડો :View Solution
કોલમ - $\mathrm{I}$ કોલમ - $\mathrm{II}$ $(a)$ શ્યાનતા બળ $(i)$ $\left[ {{M^1}{L^1}{T^{ - 2}}} \right]$ $(b)$ શ્યાનતા ગુણાંક $(ii)$ $\left[ {{M^1}{L^{ - 1}}{T^{ - 1}}} \right]$ $(iii)$ $\left[ {{M^1}{L^{ - 1}}{T^{ - 2}}} \right]$ - 7View Solutionગેજ દબાણ એ...
- 8નીચે બે વિધાનો આપ્યાં છે.View Solution
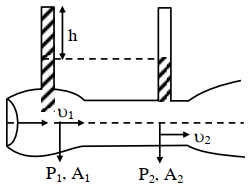
વિધાન $I$: જ્યારે પ્રવાહીની ઝડપ દરેક સ્થાને શૂન્ય હોય તો કોઈ બે બિંદૂઓ વચ્ચેનો દબાણ઼ તફ઼ાવત સમી, $P_1-P_2=\rho g\left(h_2-h_1\right)$ ઊપર આધાર રાખે છે.
વિધાન $II$ : દર્શાવેલ વેન્ચ્યુમીટરમાં $2 \mathrm{gh}=v_1^2-v_2^2$ છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય ઉત્તર પસંદ કરો :
- 9$w$ જાડાઈ ધરાવતા અને $H$ ઊંંચાઈ ધરાવતા ડેમમાં પાણી ભરવામાં આવે છે, તો ડેમ પર લાગુ પડતું પરીણામી બળ.View Solution
- 10એક બંધ નળી સાથે જોંડેલ દબાણ-મીટરમાં $4.5 \times 10^4 \mathrm{~N} / \mathrm{m}^2$ નું અવલોકન મળે છે. વાલ્વ ચાલુ કરતાં, પાણી વહેવાનું ચાલુ થાય છે અને દબાણ-મીટરમાં અવલોકન ઘટીને $2.0 \times 10^4 \mathrm{~N} / \mathrm{m}^2$ થાય છે. પાણીનો વેગ $\sqrt{\mathrm{V}} \mathrm{m} / \mathrm{s}$ માલૂમ પડે છે. $\mathrm{V}$ નું મૂલ્ય છે.View Solution
