જો કોઈ બ્લોક $5 \,m / s$.ના વેગ સાથે $30^{\circ}$ ઢોળાવવાળી સપાટી ૫ર ઊધ્વદિશામાં ગતિ કરે છે, તે $0.5 \,s$ પછી અટકી જાય છે, તો પછી ઘર્ષણાંક લગભગ કેટલું હશે ?
Easy
Download our app for free and get started
b
(b)
(b)
Using \(v=u+a t\)
retardation will be provided by friction as well as gravitational force
\(a=\frac{u}{t}\)
\(g \sin 30^{\circ}+\mu g \cos 30^{\circ}=\frac{5}{0.5}=10\)
\(\mu=\frac{1}{\sqrt{3}} \equiv 0.6\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમક્ષિતિજ સાથે $\theta$ ખૂણો બનાવતા ઢાળ $AB$ પર બિંદુ $B$ પાસેથી એક બ્લોક નીચે તરફ સરકે છે,જેમાં ઉપરનો $BC$ ભાગ લીસો અને બાકીનો $CA$ ભાગ ખરબસડો છે જેનો ઘર્ષણાંક $\mu$ છે. જ્યારે બ્લોક તળિયે બિંદુ $A$ પાસે પહોચે ત્યારે તે સ્થિર થાય છે. જો $BC=2AC$, હોય તો તેનો ઘર્ષણાંક $\mu=k \tan \theta$ વડે આપવામાં આવે છે.તો $k$ નું મૂલ્ય કેટલું હશે?View Solution
- 2એક કાર અચળ ઝડપે સાથે $0.1 \,km$ ની ત્રિજ્યાના સમક્ષિતિજ વર્તુળાકાર રસ્તા પર ગતિ કરી રહી છે. જો કારના ટાયર અને રસ્તા વચચચેનો ઘર્ષણાંક $0.4$ છે, તો કારની ઝડપ ............ $m / s$ હોઈ શકે છે $\left[g=10 \,m / s ^2\right]$View Solution
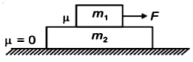
- 3આપેલી પરિસ્થિતિ માટે $F$ નું મહત્તમ મૂલ્ય શું હોઈ શકે જેથી બંને બ્લોક વચ્ચે કોઈ સાપેક્ષ ગતિ ન હોય.View Solution
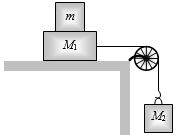
- 4${M_1}$ અને સપાટી વચ્ચેનો ઘર્ષણાંક $ \mu$ છે. જયારે તંત્રને મુકત કરવામાં આવે ત્યારે પ્રવેગીત ગતિ કરે છે. ${M_1}$ બ્લોક પર કેટલું દળ $m$ મૂકવાથી તંત્ર અચળ વેગથી ગતિ કરશે?View Solution
- 5$60\, kg$ નો માણસ થાંભલા પર $600 \,N$ બળ લગાવીને નીચે ઉતરે છે.હાથ અને થાંભલા વચ્ચેનો ઘર્ષણાંક $0.5$ હોય,તો માણસ ........ $m/s^2$ પ્રવેગ પ્રાપ્ત કરશે. $(g = 10\,\,m/{s^2})$View Solution
- 6$0.5$ ઘર્ષણાંક ધરાવતા ઢાળ પર બ્લોક મૂકતાં લંબ બળ એ પરિણામી ઢાળને સમાંતર લાગતા બળ કરતાં બમણું છે,તો ઢાળનો ખૂણો ........ $^o$ હશે.View Solution
- 7બરફ પર પડેલ $2\, kg$ ના બ્લોકને $6 \,m/s $ નો વેગ આપતાં $10\, s $ માં સ્થિર થાય,તો ઘર્ષણાંક કેટલો હશે?View Solution
- 8$25 \,kg$ વજનનો એક બાળક એક ઊંચા વૃક્ષની શાખામાં લટકાવેલી દોરીથી નીચે તરફ લપસે છે. જો તેની વિરદ્ધ $200 \,N$ જેટલું ઘર્ષણ બળ લાગતું હોઈ, તો બાળકનો પ્રવેગ ................. $m / s^2$ છે $\left(g=10 \,m / s ^2\right)$View Solution
- 9$m$ દળ ધરાવતા બ્લોક (ચોસલા)ને $y=x^2 / 4$ વડે દર્શાવેલ ઊર્ધ્વ આડછેદ ધરાવતી સપાટી પર મૂકવામાં આવે છે. જો ધર્ષણાંકનું મૂલ્ચ $0.5$ હોય તો સપાટી (ધરા)થી કે જ્યાં ચોસલું સરકે નહી તે રીતે મૂકી શકાય તે મહત્તમ ઊંચાઈ________હશે.View Solution
- 10એક છોકરો કેન્દ્રથી $5 \,m$ નાં અંતરે ચકડોળનાં સમક્ષિતિજ પ્લેટફોર્મ પર બેઠો છે. આ ચકડોળ ફરવાનું શર કરે છે અને જ્યારે કોણીય ઝડપે $1 \,rad/s$ થી વધી જાય છે, ત્યારે છોકરો ફક્ત લપસે છે. છોકરો અને ચક્ર વચ્ચેનો ઘર્ષણાંક શું છે $\left(g=10 \,m / s ^2\right)$View Solution