જો $ m_1 = 4m_2$ છે . $m_1 $ નો પ્રવેગ $a$ છે. તો દોરીમાં તણાવ $T =$ ____
Medium
Download our app for free and get started
d
\({m_1}a = {m_1}g - 2T\) …..(i)
\({m_1}a = {m_1}g - 2T\) …..(i)
\({m_2}\left( {2a} \right) = T - {m_2}g\)…..(ii)
\(a = g/4\)
\(T = \frac{3}{2}\,{m_2}g\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10^{-2}\, m^2$ આડછેડનું ક્ષેત્રફળ ધરાવતી સમક્ષિતિજ નળીમાંથી $1.5\, ms^{-1}$ ઝડપે આવતા પણે ને હથેળી વડે રોકવામાં આવે છે.પાણી હથેળીને અથડાતાં તરત ઊભું રહી જાય છે તેમ ધારતા પાણીને રોકવા ઓછામા ઓછું ........ $N$ બળ લગાવવું પડતું હશે?View Solution
- 2$5\, {kg}$ દળના પદાર્થ પર $\vec{F}=(40 \hat{i}+10 \hat{j})\, N$ જેટલું બળ લાગે છે. જો પદાર્થ સ્થિર સ્થિમાંથી ગતિની શરૂઆત કરતો હોય, તો $t=10\, {s}$ સમયે તેનો સ્થાનસદીશ $\vec{r}$ કેટલો થાય?View Solution
- 3$4 \mathrm{~kg}$ દળ ધરાવતો એક પદાર્થ બે બળો $\overrightarrow{\mathrm{F}_1}=5 \hat{i}+8 \hat{j}+7 \hat{k}$ અને $\overrightarrow{\mathrm{F}_2}=3 \hat{i}-4 \hat{j}-3 \hat{k}$ અનુભવે છે. પદાર્થમાં પ્રવેગ____________હશે.View Solution
- 4View Solutionજો તંત્ર પર લાગતું પરિણામી (Net) બળ શૂન્ય હોય તો
- 5એક $Mg$ વજનને એક દોરીનાં મધ્યમાં લટકાવવામાં આવ્યું છે જેના છેડાઓ સમાન સ્તર પર છે. દોરી હવે સમક્ષિતિજ નથી. દોરીને સંપૂર્ણપણે સીધી કરવાં માટે જરરી લઘુત્તમ તણાવ બળ છે.View Solution
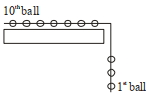
- 6દરેક $2 \,kg$ ના $10$ બોલના બનેલાં તંત્રને દળરહિત અને ખેંચી ના શકાય તેવી દોરી વડે જોડવામાં આવેલા છે. આ તંત્રને લીસા ટેબલ ઉપર આફૃતિમાં દર્શાવ્યા અનુસાર સરકવા દેવામાં આવે છે. જ્યારે છઠ્ઠો બોલ ટેબલને છોડે તે જ ક્ષણે $7^{\text {th }}$ મા અને $8^{\text {th }}$ મા બોલ વચ્યે દોરીમાં તણાવ ........... $N$ હશે.View Solution
- 7View Solutionસામાન્ય ખગોળીય પ્રયોગો માટે જડત્વ ફ્રેમ માં રહેલો અવલોકનકાર નીચેના માથી કયા કિસ્સા બરાબર છે?
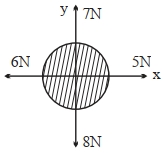
- 8આકૃતિમાં દર્શાવ્યા પ્રમાણે $free\,body\,diagram$ $(FBD)$ માટે, ઘણા બધા બળો ' $x$ ' અને ' $y$ ' દિશામાં લગાવવામાં આવે છે. વધારાનો કેટલો અને $x-$અક્ષને કેટલા કોણે બળ લગાડવો પડશે કે જેથી પદાર્થમાં પરિણામી (સમાસ) પ્રવેગ શૂન્ય થાય?View Solution
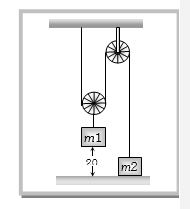
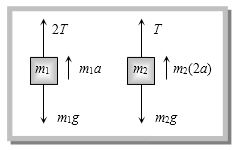
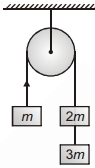
- 9નીચે આપેલી આક્રુતિમાં $m$ દળનો બ્લોક કેટલાં પ્રવેગથી ગતિ કરશે? (ગરગડી સને દોરીઓ ધર્ષણ રહિત, દળરહિત છે)View Solution
- 10એક બેટ્સમેન $0.4 \,kg$ દળ ધરાવતા બોલને પાછો બોલરની જ દિશામાં તેની પ્રારંભિક ઝ5પ $15 \,ms ^{-1}$ ને બદલ્યા વગર ફટકારે છે. બોલને આપવામાં આવતો આવેગ (બોલને રેખીય ગતિ છે તેમ ધારતાં) ......... $Ns$ હશે.View Solution