જો સમાન દળના બે કણની વક્રતા ત્રિજ્યાઓનો ગુણોત્તર $3:4$ હોય, તો તેમના કેન્દ્રગામી પ્રવેગ અચળ રહે તે માટે તેમના વેગનો ગુણોત્તર._________હોય.
JEE MAIN 2024, Diffcult
a
Given \(\mathrm{m}_1=\mathrm{m}_2\)
Given \(\mathrm{m}_1=\mathrm{m}_2\)
\(\text { and } \frac{\mathrm{r}_1}{\mathrm{r}_2}=\frac{3}{4}\)
As centripetal force \(F=\frac{\mathrm{mv}^2}{\mathrm{r}}\)
In order to have constant (same in this question) centripetal force
\( \mathrm{F}_1=\mathrm{F}_2 \)
\( \frac{\mathrm{m}_1 \mathrm{v}_1^2}{\mathrm{r}_1}=\frac{\mathrm{m}_2 \mathrm{v}_2^2}{\mathrm{r}_2} \)
\( \Rightarrow \frac{\mathrm{v}_1}{\mathrm{v}_2}=\sqrt{\frac{\mathrm{r}_1}{\mathrm{r}_2}}=\frac{\sqrt{3}}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક કારના ટાયર અને રોડ વચ્ચેનો ઘર્ષણાંક $0.5$ છે. તો કાર ની $40 \,m$ ની ત્રિજ્યા ના વળાંક વાળા રોડ પર સરક્યાં વગર ......... $m/s$ મહતમ ઝડપથી ફરી શકશે.View Solution
- 2View Solutionઅચળ કોણીય વેગથી વર્તૂળ પર ગતિ કરતાં કણ માટે નીચેનામાંથી કયું વિધાન ખોટું છે ?
- 3$2kg $ નો બ્લોક $30^o$ ના ઢાળ પર પડેલો છે જો સ્થિત ઘર્ષણાંક $0.7$ હોય તો ઘર્ષણબળ ....... $N$ થાય.View Solution
- 4$1\, kg$ ના બ્લોકને દિવાલ પર રાખવા માટે લંબબળ $F$ લગાડવામાં આવે છે.જો ઘર્ષણાક $0.2$ હોય,તો બળ $F$ નું ન્યૂનતમ મૂલ્ય ....... $N$ હોવું જોઈએ.View Solution
- 5$\theta = {30^o}$ ખૂણાવાળા ઢાળ પર બ્લોકને ઉપર તરફ $5 \,m/s $ ના ગતિ કરાવતાં તે $0.5\, sec$ સમયમાં સ્થિર થઇ જાય છે.તો ઘર્ષણાંક કેટલો હશે?View Solution
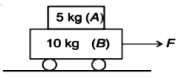
- 6જો $A$ નો પ્રવેગ $2 \,m / s ^2$ છે. જે $B$ નાં પ્રવેગ કરતાં ઓછો છે, તો $B$ વડે $A$ ઉપર લગાડવામાં આવતાં ઘર્ષણ બળનું મુલ્ય ....... $N$View Solution
- 7$'m '$ દળના એક પદાર્થ ને સ્પ્રિંગના એક છેડે બાંધીને સમક્ષિતિજ સમતલમાં અચળ કોણીય વેગથી ચક્રાકારે ફેરવવામાં આવે છે. સ્પ્રિંગમાં ખેંચાણ $1\, cm$ છે. જો કોણીય વેગ બમણો કરવામાં આવે તો સ્પ્રિંગમાં ખેંચાણ $5\, cm$ થાય છે. તો સ્પ્રિંગની મૂળ લંબાઈ ........ $cm$ હશે.View Solution
- 8View Solutionએક હોકી નો ખેલાડી ઉત્તર તરફ ગતિ કરે છે અને પ્રતિસ્પર્ધીથી દૂર રહેવા અચાનક પશ્ચિમ તરફ સમાન ઝડપે વળાંક લે છે. ખેલાડી પર લાગેલું બળ કેવું હશે?
- 9$0.5\, kg$ દળ ધરાવતાં લાકડાનાં ચોસલા અને ઊભી ખરબચડી દિવાલ વચ્ચે સ્થિત ઘર્ષણાંક $0.2$ છે. બ્લોક દિવાલ સાથે ચિપકેલો (ચોટેલો) રહે તે માટે લગાવવું પડતું સમક્ષિતિજ બળ ગણો ............. $N.$ $\left[g=10\, ms ^{-2}\right]$View Solution
- 10એક ટેબલ તેના કેન્દ્રમાંથી પસાર થતી શિરોલંબ અક્ષની આસપાસ $20\ rad/s$ ના કોણીય વેગથી ભ્રમણ કરે છે તેની પોતાની ઉપર એક ફલાય વ્હીલ જોડેલું છે જેની સમક્ષિતિજ ધરી સાથે બેરિંગ જોડેલી છે તેની આસપાસ $40\ rad/s$ થી ભ્રમણ કરે છે. વ્હીલનો પરિણામી કોણીય વેગ..... હશે.View Solution
