$'m '$ દળના એક પદાર્થ ને સ્પ્રિંગના એક છેડે બાંધીને સમક્ષિતિજ સમતલમાં અચળ કોણીય વેગથી ચક્રાકારે ફેરવવામાં આવે છે. સ્પ્રિંગમાં ખેંચાણ $1\, cm$ છે. જો કોણીય વેગ બમણો કરવામાં આવે તો સ્પ્રિંગમાં ખેંચાણ $5\, cm$ થાય છે. તો સ્પ્રિંગની મૂળ લંબાઈ ........ $cm$ હશે.
JEE MAIN 2013, Diffcult
a
Let the length of the spring is \(l\). When the system is whirled round in a horizontal circle the centripetal force is given by
Let the length of the spring is \(l\). When the system is whirled round in a horizontal circle the centripetal force is given by
\(F=\frac{m{{v}^{2}}}{r}=\frac{m{{(r\omega )}^{2}}}{r}=mr{{\omega }^{2}}\)
then \(r=l+\) elongation Given: elongation \(=1 \;cm\) (in the first case)
or angular velocity \(\omega\) the force required is
\({{F}_{1}}=m(l+1){{\omega }^{2}}=kx=k\times 1=k\)
\(k=m(l+1){{\omega }^{2}}\) .......(i)
\({{F}_{2}}=m(l+5){{(2\omega )}^{2}}=kx=k\times 5=5k\)
\(5k=4m(l+5){{\omega }^{2}}\).......(ii)
Now, dividing Eq. \((i)\) by Eq.\((ii)\), we get
\(\frac{k}{5k}=\frac{m(l+1){{\omega }^{2}}}{4m(l+5){{\omega }^{2}}}\)
\(5(l+1)=4(l+5)\)
\(l=20-5=15\,cm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$l$ લંબાઈ ધરાવતી લાકડી તેના કોઈ એક છેડામાથી પસાર થતી અક્ષને અનુલક્ષીને અચળ કોણીય ઝડપથી ભ્રમણ કરે છે.ભ્રમણના કારણે લાકડીમાં અક્ષથી $x$ અંતરે ઉત્પન્ન થતું તણાવ $T(x)$ હોય તો નીચેનામાથી કયો ગ્રાફ તણાવ માટે સાચો પડે?View Solution
- 2$200\, g$ દળ ધરાવતો બ્લોક $20\, cm$ ત્રિજ્યા ધરાવતા સમક્ષિતિજ વર્તુળમાં ભ્રમણ કરે છે. બ્લોક એક પરિભ્રમણ માટે $40\, sec$ સમય લે છે. તો દીવાલ દ્વારા લાગતું લંબ બળ કેટલું હશે?View Solution
- 3$10 \,kg$ દળનાં એક બ્લોકને ખરબચડી ઢોળાવવાળી સપાટીથી છોડવામાં આવ્યો છે. બ્લોક એ $2 \,m / s ^2$ ના પ્રવેગ સાથે નીચે તરફ ગતિ કરવાનું શરુ કરે છે. તો બ્લોક પર લાગતું ગતિક ઘર્ષણબળ ........... $N$ ( $g=10 \,m / s ^2$ લો)View Solution
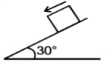
- 4આકૃતિમાં દર્શાવ્યા મુજબ $10\ kg$ દળ ધરાવતા ચોસલાને ખરબચડા ઢોળાવ પર રાખવામાં આવેલ છે. ચોલસા પર $3\ N$ બળ લગાડવામાં આવે છે. સમતલ અને ચોલસા વચ્ચે સ્થિતઘર્ષણાંક $0.6$ છે. ચોલસું નીચે તરફ ગતિ ના કરે તે માટે જરૂરી લઘુત્તમ બળ $P$ નું મૂલ્ય ........ $N$ હશે.View Solution
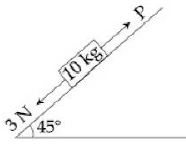
- 5View Solutionઆકૃતિમાં દર્શાવેલ બ્લોક સમતોલન સ્થિતિમાં હોય,તો બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક કેટલો થશે?
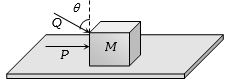
- 6$m$ દળની એક કાર $R$ ત્રિજયાના વર્તુળાકાર પથ પર ગતિ કરે છે. જો $\mu_s $ રોડ અને કારના ટાયર વચ્ચેનો સ્થિત ઘર્ષણાંક હોય, તો આ વર્તુળાકાર ગતિ દરમિયાન કારની મહત્તમ સલામત ઝડપ કેટલી હોવી જોઈએ?View Solution
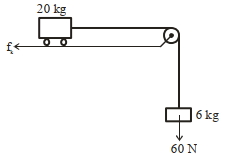
- 7આકૃતિમાં દર્શાવ્યા મુજબ એક બ્લોક અને ટ્રોલીના તંત્રને ધ્યાનમાં લો. જો ટ્રોલી અને સપાટી વચ્ચેનો ગતિક ઘર્ષણાંક $0.04$ હોય તો તંત્રનો $\mathrm{ms}^{-2}$ માં પ્રવેગ__________છે.(દોરીનું દળ અવગણો)View Solution
- 8એક ગ્રામોફોન રેકોર્ડ $\omega $ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. આ રેકોર્ડના કેન્દ્રથી $r $ અંતરે એક સિકકો મૂકેલો છે. સ્થિત ઘર્ષણાંકનું મૂલ્ય $\mu $ છે. સિકકો એ રેકોર્ડની સાથે ભ્રમણ કરશે, જો ........View Solution
- 9સમક્ષિતિજ સપાટી પર રહેલા એક ટ્રક ($\,\mu = 0.6$) પર $1\, kg$ નો બ્લોક પડેલો છે અને ટ્રકનો પ્રવેગ $ 5\,m/sec^2$ હોય, તો બ્લોક પર કેટલું ઘર્ષણ બળ ($N$ માં) લાગતું હશે?View Solution
- 10એક દોરીમાં $10 \,N$ થી વધારે બળ લાગતા,તે તૂટી જાય છે.તે દોરી પર $250 \,gm$ દળ ધરાવતો પદાર્થ બાંધીને $10\, cm$ ત્રિજયામાં ફેરવતા દોરી તૂટે નહિ,તે માટે મહત્તમ કોણીય ઝડપ .......... $rad/s$ રાખવી જોઈએ.View Solution
