$(A)\quad\quad\quad\quad(B)$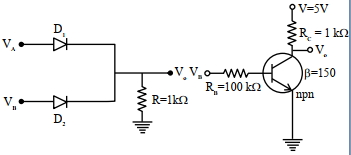
\({V}_{{A}}=5 {V} \Rightarrow {A}=1\)
\({V}_{{A}}=0 {V} \Rightarrow {A}=0\)
\({V}_{{B}}=5 {V} \Rightarrow {B}=1\)
\({V}_{{B}}=0 {V} \Rightarrow {B}=0\)
If \({A}={B}=0\), there is no potential anywhere here \({V}_{0}=0\)
If \({A}=1, {B}=0\), Diode \({D}_{1}\) is forward biased, here \({V}_{0}=5 {V}\)
If \({A}=0, {B}=1\), Diode \({D}_{2}\) is forward biased hence \({V}_{0}=5 {V}\)
If \({A}=1, {B}=1\), Both diodes are forward biased hence \({V}_{0}=5 {V}\)
Truth table for \({I}^{{st}}\)
| \(A\) | \(B\) | Output |
| \(0\) | \(0\) | \(0\) |
| \(0\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(1\) |
| \(1\) | \(1\) | \(1\) |
\(\therefore\) Given circuit is \(OR\) gate
For \(\mathbb{I}^{{Id}}\) circuit
\({V}_{{B}}=5 {V}, {A}=1\)
\({V}_{{B}}=0 {V}, {A}=0\)
When \({A}=0, {E}-{B}\) junction is unbiased there is no current through it
\(\therefore {V}_{0}=1\)
When \({A}=1, {E}-{B}\) junction is forward biased
\({V}_{0}=0\)
\(\therefore\) Hence this circuit is not gate.
Download our appand get started for free
Similar Questions
- 1જર્મેંનિયમ સ્ફટિક માટે ફોરબિડન ગૅપની પહોળાઈ આશરે ....... $J $ હોય છે.View Solution
- 2$NOR $ ગેટ મેળવવા માટે, ઓછામાં ઓછા કેટલા $NAND $ ગેટ જોઈએ ?View Solution
- 3View Solutionનીચે દર્શાવેલ વિકલ્પોમાં કયું વિધાન ખોટું છે?
- 4ફોટોડાયોડની વાહકતા ફક્ત જયારે આપાત પ્રકાશની તરંગલંબાઈ $660 \mathrm{~nm}$ થી ઓછી હોય ત્યારે બદલાય છે. ફોટોડાયોડ માટે બેન્ડ ગેપ $\left(\frac{X}{8}\right) \mathrm{eV}$ જેટલો મળે છે, તો $X$ નું મૂલ્ય_________છે.View Solution
$\text { ( } \mathrm{h}=6.6 \times 10^{-34} \mathrm{Js}, \mathrm{e}=1.6 \times10^{-19}\mathrm{C}$આપેલ છે.
- 5View Solutionજ્યારે સિલિકોનમાં આર્સેનિકની અશુધ્ધિ ઉમેરવામાં આવે તો પરિણામી પદાર્થ કેવો બને?
- 6View Solutionઝેનર ડાયોડ માટે સાચું વિધાન પસંદ કરો.
- 7નીચે આપેલ સત્યાર્થ કોષ્ટક કયો લોજીક ગેટ દર્શાવે છે ?View Solution
$A$
$B$
$Y$
$0$
$0$
$0$
$0$
$1$
$1$
$1$
$0$
$1$
$1$
$1$
$0$
- 8View Solutionરેકિટફાયરનું શું કાર્ય કરે?
- 9ઝેનર ડાયોડમાં બ્રેક ડાઉન વોલ્ટેજ $9.1V$ મહત્તમ વિદ્યુત વિતરણ દ્વારા $364\; mW$ છે. તો ડાયોડમાં મહત્તમ કેટલા .......$ mA$ વિદ્યુતપ્રવાહ મેળવી શકાય?View Solution
- 10View Solutionડિપ્લેશન સ્તરમાં પોટેન્શિયલ બેરિયર કોના કારણે હોય?
