જ્યારે $4 \,kg$ ની રાઈફલને છોડવામાં આવે છે, તો $10 \,g$ ની ગોળી $3 \times 10^6 \,cm / s ^2$ નો પ્રવેગ મેળવે છે. રાઈફલ પર લાગતું બળનું મૂલ્ય (ન્યુટનમાં) છે
Easy
Download our app for free and get started
c
(c)
(c)
Using Newton's third law, bullet will apply the same force in the opposite direction.
So, using \(F=m a=\frac{10}{1000} \times 3 \times 10^6 \times 10^{-2}=300 \,N\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્થિર સ્થિતિમાં રહેલું $3 \times {10^7}\,kg$ નું જહાજ પર $5 \times {10^4}\,N$ બળ લાગતા $3\;m$ અંતર કાપે છે. જો પાણી દ્વારા લાગતો અવરોધ નહિવત હોય તો જહાજની ઝડપ ........... $m/s$ થશે.View Solution
- 2View Solutionઆકૃતિમાં દર્શાવ્યા મુજબ બે દળ ધરાવતા પદાર્થોને હલકી પુલી પરથી લટકાવેલ છે. જયારે પદાર્થને મુકત કરવામાં આવે ત્યારે તંત્રનો પ્રવેગ કેટલો થશે?
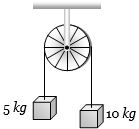
- 3એક કણનો વેગમાન $p\left( kg m / s\right)$ માં એ સમય $t$ ($s$ માં) સાથે $p=2+3 t^2$ મુજબ બદલાય છે. તો $t=3 s$ એ કણ પર લગાડવામાં આવતું બળ ........... $N$ હશે.View Solution
- 4$2000 \,kg$ ની કાર પર બંદુક મૂકીને $1\, sec$ માં $10$ ગોળી છોડવામાં આવે છે.ગોળીનું દળ $10\, gm$ અને વેગ $500 \,m/s $ હોય,તો કાર પર ........ $N$ બળ લાગતું હશે.View Solution
- 5એક કણ $\overrightarrow{\mathrm{F}}$ બળની અસર હેઠળ $x-y$ સમતલમાં એવી રીતે ગતિ કરે છે કે તેનું રેખીય વેગમાન $\overrightarrow{\mathrm{p}}(\mathrm{t})=\hat{i} \cos (\mathrm{kt})-\hat{j} \sin (\mathrm{kt})$ થી આપી શાકા છે. જો $\mathrm{k}$ એ અચળાંક હોય તો $\overrightarrow{\mathrm{F}}$ અને $\overrightarrow{\mathrm{p}}$ વચ્ચેનો કોણ. . . . . . . .થશે.View Solution
- 6આપેલ આકૃતિમાં, $2\,kg$ અને $1\,kg$ વચ્ચે સંપર્ક બળ ........ $N$ હશે? (સપાટીને લિસી લો.) (આપેલ : $g =10 \,ms ^{-2}$)View Solution
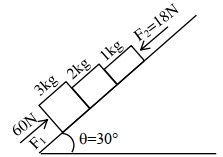
- 7$m$ દળનો કણ $u $ વેગથી $ m$ દળના સ્થિર કણ સાથે અથડાય છે,સંપર્ક સમય $T$ માટે સંપર્ક બળ આકૃતિ મુજબ લાગે છે.તો $F_0$ નું મૂલ્ય કેટલું થશે?View Solution
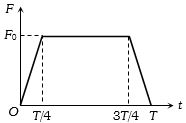
- 8લિફ્ટમાં સ્પ્રિંગ બેલેન્સ પર $2\, kg$ નો દળ લટકાવેલ છે. હવે લિફ્ટ $2 \,m/sec^2$ ના પ્રવેગથી ઉપર તરફ ગતિ કરે, તો સ્પ્રિંગ બેલેન્સનું અવલોકન ....... $kg$ હશે.View Solution
- 9$2000 \,kg$ ની કાર પર બંદુક મૂકીને $1\, sec$ માં $10$ ગોળી છોડવામાં આવે છે.ગોળીનું દળ $10\, gm$ અને વેગ $500 \,m/s $ હોય,તો કાર પર ........ $N$ બળ લાગતું હશે.View Solution
- 10એક માણસ એક હલકી દોરીથી નીચે લપસી રહ્યો છે જેની તૂટવાની શક્તિ એે માણસની વજનથી $\eta\;(\eta < 1)$ ગણી છે. તો માણસનો મહત્તમ પ્રવેગ શોધો કે જેથી દોરી તરત તૂટી જશે.View Solution