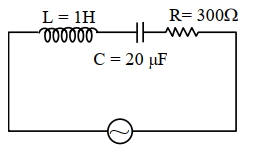
જયારે $R$ અવરોધને $AC$ ઉદ્ગમ સાથે જોડીએ ત્યારે, તે $P$ પાવર ખેંચે છે. જો અવરોધ સાથે ઇન્ડકટન્સને શ્રેણીમાં જોડતાં પરિપથનો ઇમ્પિેડન્સ $Z$ થતો હોય, તો હવે કેટલો પાવર ખેંચાશે?
AIPMT 2015, Medium
a
Case \(I:\) \(P=V_{\text {rms }} I_{\text {rms }}\)
Case \(I:\) \(P=V_{\text {rms }} I_{\text {rms }}\)
\(=V_{\mathrm{rms}} \times \frac{V_{\mathrm{rms}}}{R}\)
\(P=\frac{V_{\mathrm{rms}}^{2}}{R} \Rightarrow V_{\mathrm{ms}}^{2}=P R \ldots .(\mathrm{i})\)
Case \(II :\) Power drawn in \(L R\) circuit
\(P^{\prime}=V_{\mathrm{rms}} I_{\mathrm{rms}} \cos \phi=V_{\mathrm{rms}} \times \frac{V_{\mathrm{rms}}}{Z} \times \frac{R}{Z}\)
\(=V_{\mathrm{rms}}^{2} \frac{R}{Z^{2}}=P R \times \frac{R}{Z^{2}}\)
[Using eqn \((\mathrm{i})]\)
\(P^{\prime}=P \frac{R^{2}}{Z^{2}}\)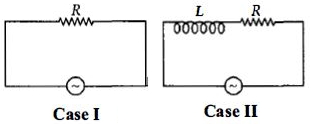
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ઈન્ડકટર ધરાવતો પરિપથ $10$ ઓહમનો અવરોધ અને $20$ હેન્રીનું ઈન્ડકટન્સ ધરાવે છે. જો આ પરિપથમાં $120\; V$ અને $60\;Hz$ આવૃત્તિનો ઓલ્ટરનેટિંગ વિદ્યુત ધ્રવાહ લગાડવામાં આવે, તો પરિપથ વિદ્યુતપ્રવાહ ($A$) આશરે કેટલો હશે ?View Solution
- 2$0.5\,H$ ઇન્કટર અને $8 \mu F$ કેપેસિટરને શ્રેણીમાં $ A.C$. વોલ્ટેજ સાથે લગાવેલ છે,$A.C.$ વોલ્ટેજની કઇ આવૃત્તિ માટે પ્રવાહ મહત્તમ થાય?View Solution
- 3View Solutionખોટું વિધાન પસંદ કરો.
- 4મૂલ્ય $R$ ધરાવતા અવરોધમાં વિદ્યુતસ્થિતિમાન $V=V_0$ $\cos \omega t$ લગાડવામાં આવે તો અવરોધમાં પ્રત્યેક ચક્ર દરમિયાન વ્યય થતો સરેરાશ પાવર કેટલો છે?View Solution
- 5$10\,H$ નું આત્મપ્રેરણ, $10\,\mu F$ ની સંધારકતા અને $50\,\Omega$ નો અવરોધ ધરાવતા એક શ્રેણી LCR પરિપથને $V=200 \sin (100 t)$ વોલ્ટ ધરાવતા $ac$ ઉદ્રગમ સાથે જોડવામાં આવે છે. જો $LCR$ પરિપથની અનુનાદીય આવૃત્તિ $\nu_{0}$ હોય અને $ac$ ઉદ્દગમની આવૃત્તિ $\nu$ હોય તો$.......$View Solution
- 6નીચે બે કથન આપેલ છે.View Solution
કથન $I$: જ્યારે $LCR-$શ્રેણી પરિપથમાં જ્યારે આવૃત્તિ વધે છે, પરિપથમાં પહેલા પ્રવાહ વધે છે, મહત્તમ મૂલ્ચ પ્રાપ્ત કરે છે. અને ત્યાર બાદ ધટે છે.
કથન $II$ : શ્રેણી $LCR$ પરિપથમાં અનુવાદ વખતે પાવર અવયવનું મૂલ્ય એક હોય છે.
ઉપર્યુક્ત બંને કથનના સંદર્ભમાં, નીચે આપેલ વિકલ્પોમાંથી સાયો ઉત્તર પસંદ કરો.
- 7$100\,\Omega$ અવરોધનો અવરોધક, $1\,H$ ઈન્ડકટન્સનો ઈન્ડકટર અને $6.25\,\mu F$ કેપેસીટન્સ (સંધારકતા) નો સંધારક (કેપેસીટર) એસી ઉદગમ સાથે શ્રેણીમાં જોડેલા છે. પરિપથનો કવોલીટી અવયવ ......... હશે.View Solution
- 8ખૂબ ઊંચી આવૃતિ માટે આપેલ પરિપથનો ઇમ્પીડન્સ ($\Omega$ માં) કેટલો હોવો જોઈએ?View Solution
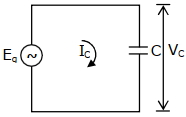
- 9આપેલ પરિપથમાં કેપેસીટર અને $E_{g}=E_{g0}\,sin\omega t$ જેટલો પ્રત્યાવર્તી $emf$ ધરાવતું જનરેટર છે, $V_{C}$ અને ${I}_{{C}}$ વૉલ્ટેજ અને પ્રવાહ છે.આ પરિપથ માટે સાચો ફેઝર ડાયાગ્રામ કેવો થાય?View Solution
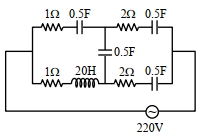
- 10આપેલ શ્રેણ઼ી $LCR$ પરિપથસાથે $ac$ ઉદગમ જોડવામાં આવેલ છે. $20 \mu \mathrm{F}$ સંધારક (કેપેસીટર)ને સમાંતર $rms$ સ્થિતિમાનનો તફાવત. . . . . . . . . $\mathrm{V}$ હશે.View Solution