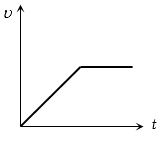
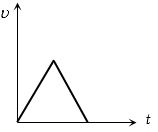
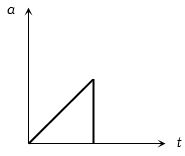
કણ માટે પ્રવેગ વીરૂધ સમયનો ગ્રાફ આપેલ છે તો તેના માટે વેગ વિરૂધ સમયનો ગ્રાફ કેવો મળે?

Diffcult
c
(c) From given \(a - t\) graph it is clear that acceleration is increasing at constant rate
(c) From given \(a - t\) graph it is clear that acceleration is increasing at constant rate
\(\therefore \) \(\frac{{da}}{{dt}} = k\) (constant) \(⇒\) \(a = kt\) (by integration)
\(⇒ \frac{{dv}}{{dt}} = kt\) \(⇒\) \(dv = ktdt\)
\(⇒ \int_{}^{} {dv} = k\int_{}^{} {tdt} \) \(⇒\) \(v = \frac{{k{t^2}}}{2}\)
i.e. \(v\) is dependent on time parabolically and parabola is symmetric about v-axis.
and suddenly acceleration becomes zero. i.e. velocity becomes constant.
Hence \((c)\) is most probable graph.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$20\;m$ મીટર ઊંચાઇના ટાવર પરથી એક છોકરો પથ્થરને છોડે છે. $g = 10 \,ms^{-2,}$ ધારતા, તે જમીન સાથે અથડાય ત્યારે તેનો વેગ ($ms^{-1}$ માં) કેટલો હશે?View Solution
- 2$d$ ઊંચાઇના ટાવર પરથી એક બોલને મુકત કરવામાં આવે છે.તે જમીન સાથે અથડાઇને $d/2$ ઊંચાઇ સુધી જાય છે.તો બોલનો વેગ વિરુધ્ધ ઊંચાઇનો આલેખ કેવો મળે?View Solution
- 3એક ટ્રેન $60 km/hr$ ની ઝડપથી પ્રથમ કલાક અને $40 km/hr$ ની ઝડપથી અડધો કલાક ગતિ કરે ,તો સરેરાશ ઝડપ કેટલા..........$km/h$ થાય?View Solution
- 4સ્થિર સ્થિતિમાંથી કાર $a$ પ્રવેગથી $t=0$ થી $t=T$ સુધી ગતિ કરે છે.પછી પ્રતિપ્રવેગથી સ્થિર થઇ જાય છે તો તેની સરેરાશ ઝડપ કેટલી થાય?View Solution
- 5એક કણ સીધી રેખામાં ગતિ કરે છે અને તેની સ્થિતિ $x$ એ સમયે $x^2=2+t$ દ્વારા આપવામાં આવે છે. તેનો પ્રવેગ શેના દ્વારા આપવામાં આવે છે?View Solution
- 6એક બાળક $6 \,km$ દૂર આવેલી સ્કૂલે $2.5\, km/hr$ અને $4 \,km/hr$ ની ઝડપે ઘરે પાછો આવે છે,તો સરેરાશ ઝડપ કેટલી થાય?View Solution
- 7View Solutionપદાર્થનું સ્થાનાંતર તેના દ્વારા લાગતાં સમયના ધનના સમપ્રમાણ હોય તો પદાર્થના પ્રવેગનું મૂલ્ય .....
- 8એક બસ સીધા રસ્તા પર $10\ ms^{-1 }$ ની ઝડપે ગતિ કરે છે. એક સ્કૂટરસવાર એ બસને $ 100s$ માં ઓવરટેક કરવા માગે છે. જો બસ સ્કૂટરસવારથી $1 \ km$ ના અંતરે હોય, તો સ્કૂટરસવારે કેટલી ઝડપે $(m/s$ માં$)$ બસનો પીછો કરવો જોઈએ?View Solution
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે પદાર્થ અનુક્રમે $AB, BC$ અને $CD$ રેખાખંડ પર $v_1, v_2$ અને $v_3$ ઝડપથી ગતિ કરે છે. જ્યાં $AB = BC$ અને $AD =3 AB$, તો પદાર્થની સરેરાશ ઝડપ કેટલી હશે?View Solution
- 10આકૃતિમાં દર્શાવેલાં બ્લોક એ $10 \,m / s$ નાં અચળ વેગે જમણી બાજુ તરફ ગતિ કરે છે. સંપર્કમાંની તમામ સપાટીઓ ખરબચડી છે. બ્લોક $B$ પર જમીન દ્વારા લગાડેલું ઘર્ષણ બળ ..... $N$ છેView Solution