કોમન એમિટર ટ્રાન્ઝીસ્ટર માટે આઉટપુટ અવરોધ $500\,k\Omega $, પ્રવાહ ગેઈન $\alpha = 0.98$ અને પાવર ગેઈન $6.0625 \times 10^6$ હોય તો ઈનપુટ અવરોધ ........ $\Omega $
AIIMS 2008, Diffcult
a
\(R_{0}=500\, \mathrm{k\Omega} ; \alpha=0.98\)
\(R_{0}=500\, \mathrm{k\Omega} ; \alpha=0.98\)
Power gain \(=6.0625 \times 10^{6}\)
we have, voltage gain \(\mathrm{A}_{\mathrm{V}}=\beta \cdot \frac{\mathrm{R}_{0}}{\mathrm{R}_{\mathrm{i}}}\)
But current gain,
\(\beta=\frac{\alpha}{1-\alpha}=\frac{0.98}{1-0.98}=49\)
\(\therefore A_{V}=49 \times \frac{500 \times 10^{3}}{R_{i}}=\frac{24.5 \times 10^{6}}{R_{i}}\)
Given \(6.0625 \times 10^{6}=\mathrm{A}_{\mathrm{V}} \times \beta\)
\(=\left(\frac{24.5 \times 10^{6}}{\mathrm{R}_{\mathrm{i}}}\right) \times 49\)
or \(\quad \mathrm{R}_{\mathrm{i}}=\frac{24.5 \times 49}{6.0625}=198 \,\Omega\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચે આપેલ ટ્રુથ ટેબલ કયા ગેટ માટેનું છે?View Solution
$A$ $B$ $Y$ $0$ $0$ $0$ $0$ $1$ $1$ $1$ $0$ $1$ $1$ $1$ $1$ - 2જ્યારે ડાયોડ ફોરવર્ડ બાયસમાં હોય ત્યારે વૉલ્ટેજ $0.5\, V$ છે,ડાયોડનો સુરક્ષિત પ્રવાહ $10\, mA$ છે.ડાયોડને $1.5\, V$ ની બેટરી સાથે જોડવામાં માટે તેની સાથે શ્રેણીમાં જોડવો પડતો અવરોધ $.....\Omega$View Solution
- 3ટ્રાન્ઝિસ્ટરમાં $\alpha$ અને $\beta$ કેટલા હોય?View Solution
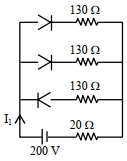
- 4આકૃતિમાં રહેલ દરેક ડાયોડનો ફોરવર્ડ બાયસનો અવરોધ $30\, \Omega$ અને રિવર્સ બાયસનો અવરોધ અનંત છે. પ્રવાહ ${I}_{1}$ ($A$ માં) કેટલો હશે?View Solution
- 5કાર્બન, સિલિકોન અને જર્મેનિયમ અણુઓમાં ચાર વેલેન્સ ઇલેક્ટ્રોન હોય છે. તેઓ તેમના વેલેન્સ બેન્ડ અને કન્ડકન બેન્ડ ઊર્જા સ્તર દ્વારા અલગ પડે છે. આ ઊર્જા સ્તર અનુક્રમે $(E_g)_C, (E_g)_{Si}$ અને ${({E_g})_{Ge}}$ દ્વારા સૂચવવામાં આવે છે. આ કિસ્સામાં નીચેનામાંથી કયો સંબંધ સાચો છે?View Solution
- 6એક $N - P - N$ ટ્રાન્ઝિસ્ટર પરિપથમાં કલેક્ટર પ્રવાહ $10\;mA$ છે. જો ઉત્સર્જાયેલા ઈલેક્ટ્રોનમાંથી $90\%$ કલેક્ટર સુધી પહોચતાં હોય, તો.....View Solution
- 7$NPN$ ટ્રાન્ઝિસ્ટરનો એમ્પ્લિફાયર તરીકે ઉપયોગ થાય જ્યારે .....View Solution
- 8શુદ્ધ સેમિકંડક્ટરમાં ઇલેક્ટ્રોન અને દોલનોની સંખ્યા ઘનતા $10^{16} m ^{-3}$ છે. ગેલિયમ ઉમેરતા $n _{ h }=5 \times 10^{22} m ^{-3}$ થાય તો, $n _{ e } = ......$View Solution
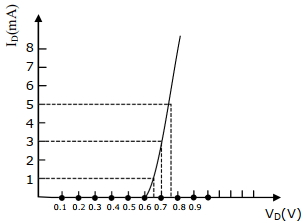
- 9આકૃતિમાં ફોરવર્ડ બાયસની લાક્ષણિક્તા દર્શાવેલ છે, તો ${I}_{{D}}=3 \,{mA}$ પ્રવાહે અવરોધ ($\Omega$ માં) કેટલો હશે?View Solution
- 10એ લોજીક-ગેટ પરિપથને બે ઈનપુટ $A$ અને $B$ અને આઉટપુટ $Y$ છે. $A$ અને $B$ આગળના તરંગ (વોલ્ટેજ) નીચે દર્શાવવામાં આવ્યા છે.View Solution