(d)
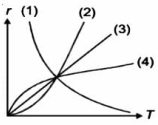
Consider a satellite of mass \(M\) revolving in a circular orbit around the earth, which is located at the center of its orbit. If a satellite is at height \(h\) above earths surface the radius of the orbit \(r = R _e\) th where \(R _e\) is radius of earth. The gravitational force between \(M _e\) and \(M\) provides the centripetal force for circular motion
or \(V ^2=\frac{ GM _e}{ R _e+ h } \quad V =\sqrt{\frac{ GM _e}{ R _e+ h }}\)
Hence orbital velocity depends on height of the satellite above earth's surface. Time period if satellite is time taken to complete one revolution.
\(T =\frac{2 \pi r }{ V }=2 \pi\left( R _{ e }+ h \right)\)
\(\sqrt{ Re _{ e }+ h } / GM _{ e }\)
\(T ^2=\frac{4 \pi^2\left( R _e+ h \right)^3}{ GM _e}\) where \(r = R _{ e }+ h\)
Download our appand get started for free
Similar Questions
- 1સમાન દળનાં બે ઉપગ્રહો પૃથ્વીની આસપાસ વિવિધ અર્ધ દીર્ધ અક્ષ ધરાવતી દીર્ધવૃત્તિય કક્ષામાં પરિભ્રમણ કરી રહ્યો છે. જો તેમનો પૃથ્વીના કેન્દ્રને અનુલક્ષીને કોણીય વેગમાનનો ગુણોત્તર $3: 4$ હોય, તો તેમની ક્ષેત્રીય વેગ નો ગુણોત્તર કેટલો છે ?View Solution
- 2બે ઉપગ્રહ $A$ અને $B$ જેની કક્ષીય ત્રિજ્યા $4R$ અને $R$ છે જો $A$ ઉપગ્રહ નો વેગ $3v$ હોય તો $B$ ઉપગ્રહનો વેગ કેટલો થાય?View Solution
- 3જ્યારે ઉપગ્રહ પૃથ્વીની સપાટીથી $h$ ઊંચાઈએ વર્તુળાકાર કક્ષામાં પરિભ્રમણ કરતો હોય, ત્યારે તેનું કોણીય વેગમાન $L$ છે. જો ઉપગ્રહનું પૃથ્વીના કેન્દ્રથી અંતર તેના મૂળ મૂલ્ય કરતા આઠ ગણું કરવામાં આવે, તો નવું કોણીય વેગમાન $........\,L$ થાય.View Solution
- 4પૃથ્વીની સપાટીની તદ્ન નજીક રહીને પૃથ્વીની આસપાસ અચળ કોણીય ઝડપથી $m$ દળનો ઉપગ્રહ ભ્રમણ કરે છે.તેની કક્ષીય ત્રિજયા $R_o$ અને પૃથ્વીનું દળ $M$ હોય,તો ઉપગ્રહનું કોણીય વેગમાન પૃથ્વીના કેન્દ્રને અનુલક્ષીને કેટલું થાય?View Solution
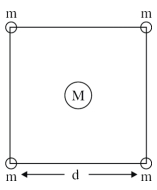
- 5$m$ દળ ધરાવતા ચાર ગોળાઓ $d$ બાજુ (આકૃતિમાં દર્શાવ્યા અનુસાર)નું ચોરસ બનાવે છે. એક પાંચમો $M$ દળ ધરાવતી ગોળો ચોરસના કેન્દ્ર આગળ મૂકવામાં આવે છે. તંત્રની કુલ સ્તિથિ ઊર્જા ........... થશે.View Solution
- 6નીચે બે વિધાનો આપેલા છે : એકને કથન $A$ અને બીજાને કારણ $R$ વડે દર્શાવેલ છે.View Solution
કથન $A$ : જ્યારે આપણે ધ્રુવથી વિષુવવૃત્ત તરફ ગતિ કરીએ છીએ, પૃથ્વીનો ગુરુત્વાકર્ષી પ્રવેગની દિશા સહેજ વિચલિત થયા વગર, હંમેશા પૃથ્વીના કેન્દ્ર તરફ જ રહે છે.
કારણ $R$ : વચ્યેના કોઈ અક્ષાંસ (Latitude) આગળ, પૃથ્વીની ગુરુત્વાકર્ષી પ્રવેગની દિશા પૃથ્વીના કેન્દ્રથી વિચલિત થાય છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 7પૃથ્વીને ફરતે આપેલ કક્ષામાં પરિક્રમણ કરતા ઉપગ્રહની આવર્તકાળ $7$ કલાક છે. જો કક્ષાની ત્રિજ્યા તેની અગાઉના મૂલ્ય કરતાં ત્રણ ગણી વધારવામાં આવે તો ઉપગ્રહનો નવો આવર્તકાળ કેટલો થશે ?View Solution
- 8એક ગ્રહ સૂર્યની આજુબાજુ $r$ ત્રિજયાની કક્ષામાં ભ્રમણ કરે છે. તેનો આવર્તકાળ $T$ છે ગ્રહ અને સૂર્ય વચ્ચે લાગતું બળ $r^{-3 / 2}$ ના સમપ્રમાણમાં હોય તો આવર્તકાળનો વર્ગ કોના સમપ્રમાણમાં હોય?View Solution
- 9${v_e}$ અને ${v_p}$ એ પૃથ્વી અને એક બીજા ગ્રહની(જેની ત્રિજ્યા પૃથ્વીની ત્રિજ્યા કરતાં બમણી છે અને ઘનતા પૃથ્વીની ઘનતા જેટલી) નિષ્ક્રમણ ઝડપ છે તોView Solution
- 10View Solutionપૃથ્વીની સરેરાશ ઘનતા ________
