$L$ લંબાઈ અને $M$ દળ ધરાવતા સળિયા $A B$ ની રેખીય ઘનતા $A$ થી $B$ તરફ જતાં $\lambda( x )=\lambda_{0}\left(1+\frac{ x }{ L }\right)$ જ્યાં, $x$ એ $A$થી અંતર છે ,તો $A$ માંથી પસાર થતી અન સળિયાને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $......ML^{2}$
JEE MAIN 2020, Diffcult
d
\(I =\int r ^{2} dm =\int x ^{2} \lambda dx\)
\(I =\int r ^{2} dm =\int x ^{2} \lambda dx\)
\(I =\int_{0}^{ L } x ^{2} \lambda_{0}\left(1+\frac{ x }{ L }\right) dx\)
\(I=\lambda_{0} \int_{0}^{L}\left(x^{2}+\frac{x^{3}}{L}\right) d x\)
\(I=\lambda\left[\frac{L^{3}}{3}+\frac{L^{3}}{4}\right]\)
\(I =\frac{7 L ^{3} \lambda_{0}}{12}\) \(...(i)\)
\(M=\int_{0}^{L} \lambda \cdot d x=\int_{0}^{L} \lambda_{0}\left(1+\frac{ x }{ L }\right) dx\)
\(M=\lambda_{0}\left(L+\frac{L}{2}\right)=\lambda_{0} \frac{3 L}{2}\)
\(\frac{2}{3} M =\left(\lambda_{0} L \right)\)\(...(ii)\)
\(From\) \((i)\) \(\&\) \((ii)\)
.\(I=\frac{7}{12}\left(\frac{2}{3} M\right) L^{2}=\frac{7 M L^{2}}{18}\)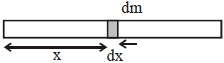
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક લીસો ગોળો $A$ ઘર્ષણરહીત સમક્ષીતિજ સપાટી પર કોણીય વેગ $\omega$ તથા દ્રવ્યમાન કેન્દ્રના વેગ સાથે ગતિ કરે છે. તે બીજા સમાન ગોળા $B$ સાથે સ્થીતિસ્થાપક સંઘાત અનુભવે છે. દરેક જગ્યાએ ઘર્ષણ અવગણતા સંઘાત બાદ તેમની કોણીય ઝડપ $\omega_A$ અને $\omega_B$ હોય તો......View Solution
- 2બે તકતીની પોતાના સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા અનુક્રમે ${I}_{1}$ અને ${I}_{2}$ છે. તેમની કોણીય ઝડપ અનુક્રમે $\omega_{1}$ અને $\omega_{2}$ છે અને તેમની એક્ષાને એક કરી દેવામાં આવે તો આ પ્રક્રિયામાં તંત્રની ગતિઊર્જામાં થતો ઘટાડો કેટલો હશે?View Solution
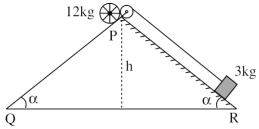
- 3$12 \,kg$ નું એક ગગડતું પૈડું ઢળતા સમતલ (ઢોળાવ) પર $P$ સ્થાને છે અને દોરી અને પુલી વડે $3 \,kg$ ના દળ સાથે આકૃતિમાં દર્શાવ્યા અનુસાર જોડેલ છે. ધારો કે $PR$ એ ધર્ષણરહિત સપાટી છે. જ્યારે વ્હીલ ઢોળાવમાં $PQ$ ના તળિયે $Q$ આગળ પહોંચે છે ત્યારે તેના ટ્રવ્યમાન કેન્દ્રની વેગ $\frac{1}{2} \sqrt{x g h} \,m / s$ છે. $x$ નું મૂલ્ય ..............View Solution
- 4View Solutionએક કણ વધતી ઝડપ સાથે સીધી રેખામાં ગતિ કરી રહ્યો છે. આ રેખા ૫ર એક સ્થિર બિંદુને અનુલક્ષીને તેનું કોણીય વેગમાન શું હશે?
- 5બે સમઅક્ષીય તકતી જેની જડત્વની ચાકમાત્રા અનુક્રમે $I_1$ અને $I_2$ છે જે અનુક્રમે $\omega_1$ અને $\frac{\omega_1}{2}$ કોણીય વેગથી તેમની સામાન્ય અક્ષને અનુલક્ષીને ભ્રમણ કરે છે. જ્યારે તેમને એકબીજાના સંપર્કમાં લાવવામાં આવે ત્યારે તે સમાન કોણીય વેગથી ગતિ કરે છે. જો $E_f$ અને $E_i$ તેમની અંતિમ અને શરૂઆતની કુલ ઉર્જા હોય તો $(E_f -E_i)$ કેટલું થાય?View Solution
- 6એક એન્જિનની મોટર પોતાની ધરીને અનુલક્ષીને $100\ rpm$ ની કોણીય ઝડપે ફરે છે. તેની સ્વિચ બંધ કરતાં $15\ s$ માં સ્થિર થાય છે, તો તે ....... પરિભ્રમણો બાદ સ્થિર થઈ હશે .View Solution
- 7$3 \ kg-m^2$ જડત્વની ચાકમાત્રા ધરાવતો પદાર્થ $2\ rad/sec$ ની કોણીય ઝડપથી ભ્રમણ કરે છે. $12\ kg$ ના પદાર્થની ગતિઊર્જા સમાન કરવા માટે .......... $m/s$ વેગથી ગતિ કરાવવો પડે.View Solution
- 8$'m'$ દળનું એક નિયમિત ઘન નળાકારીય રોલર કોઈ સમક્ષિતિજ સપાટી પર સપાટીને સમાંતર બળ $F$ રોલરના કેન્દ્ર પર લગાડીને તેને ખેંચવામાં આવે છે. જો નળાકારનો પ્રવેગ $'a'$ હોય અને તે સરક્યાં વગર દડતું હોય તો $'F'$ ની કિંમત શું થાય?View Solution
- 9$l$ બાજુની લંબાઈ ધરાવતી ચોરસ પ્લેટના એક ખૂણામાંથી પસાર થતી અને સમતલને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 10$m$ દળ ના એક બિંદુવત્ પદાર્થ ને $x$ - અક્ષના $(a, 0)$ બિંદુ પર મુક્વામાં આવે છે, તો $(-3 a, 0)$ બિંદુ પર કેટલું દળ મૂકવું જોઈએે કે જેથી દ્રવ્યમાન કેન્દ્રએ ઊગમબિંદુુ પર મળે ?View Solution
