બે તકતીની પોતાના સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા અનુક્રમે ${I}_{1}$ અને ${I}_{2}$ છે. તેમની કોણીય ઝડપ અનુક્રમે $\omega_{1}$ અને $\omega_{2}$ છે અને તેમની એક્ષાને એક કરી દેવામાં આવે તો આ પ્રક્રિયામાં તંત્રની ગતિઊર્જામાં થતો ઘટાડો કેટલો હશે?
JEE MAIN 2021, Diffcult
c
From conservation of angular momentum we get
From conservation of angular momentum we get
\({I}_{1} \omega_{1}+{I}_{2} \omega_{2}=\left({I}_{1}+{I}_{2}\right) \omega\)
\(\omega=\frac{{I}_{1} \omega_{1}+{I}_{2} \omega_{2}}{{I}_{1}+{I}_{2}}\)
\({k}_{{i}}=\frac{1}{2} {I}_{1} \omega_{1}^{2}+\frac{1}{2} {I}_{2} \omega_{2}^{2}\)
\({k}_{{f}}=\frac{1}{2}\left({I}_{1}+{I}_{2}\right) \omega^{2}\)
\({k}_{{i}}-{k}_{{f}}=\frac{1}{2}\left[{I}_{1} \omega_{1}^{2}+{I}_{2} \omega_{2}^{2}-\frac{\left({I}_{1} \omega_{1}+{I}_{2} \omega_{2}\right)^{2}}{{I}_{1}+{I}_{2}}\right]\)
Solving above we get
\({k}_{{i}}-{k}_{{f}}=\frac{1}{2}\left(\frac{{I}_{1} {I}_{2}}{{I}_{1}+{I}_{2}}\right)\left(\omega_{1}-\omega_{2}\right)^{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઘર્ષણ રહિત પુલીને વીટાળેલા દોરીના છેડે દળ લટકાવેલ છે. પુલીનું દળ $ m $ અને ત્રિજ્યા $ R$ છે. પુલી એ નિયમિત વર્તૂળાકાર તકતી હોય અને દોરા પુલી સર સરકતી ના હોય, તો દળનો પ્રવેગ .......View Solution
- 2$R$ ત્રિજયા અને $M$ દળ ધરાવતું ડ્રમ $\theta$ ખૂણાવાળા ઢાળ પર સરક્યાં વગર ગબડે છે. ઘર્ષણ બળના કારણે .....View Solution
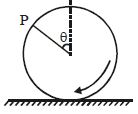
- 3એક પૈડું સરક્યાં વગર ગબડે છે. તેની અક્ષનો વેગ $v$ છે. તો પરિઘ પર રહેલ બિંદુ $P$ જે $\theta $ ખૂણે છે તે બિંદુ $P$ નો જમીનની સાપેક્ષે તત્કાલિન વેગ કેટલો હશે?View Solution
- 4કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ તેવી અક્ષને અનુલક્ષીને એક પાતળી નિયમિત તકતીની ચક્રાવર્તન ત્રિજ્યા અને તકતીના વ્યાસને ફરતે ચક્રાવર્તન ત્રિજ્યાનો ગુણોતર $......$ હશે.View Solution
- 5એક નક્કર ગોળાકાર માટે $\theta$ ખૂણો ધરાવતાં એક ઢોળાવયુક્ત સમતલ પરથી સરક્યાં વિના ગબડવા માટેનો લઘુત્તમ ઘર્ષણાંક શું હશે?View Solution
- 6એક સંતુલન ત્રાજવું અસમાન લંબાઈના હાથ ધરાવે છે. જો પદાર્થ ને એક તવી (ત્રાજવાનું પાન) માં રાખતા વજન $18 \,kg$ થાય અને બીજી તવીમાં રાખતા વજન $8 \,kg$ થાય તો પદાર્થનું સાચું વજન ........ $kg$ થાય.View Solution
- 7એક પદાર્થ એક સ્થિર અક્ષને અનુલક્ષીને $3 \,rad / s ^2$ ના કોણીય પ્રવેગ સાથે ભ્રમણ કરે છે. જે સમયે તેનો કોણીય વેગ $10 \,rad / s$ માંથી. વધી ને $20 \,rad / s$ થાય તે સમય દરમિયાન તેના દ્વારા ભ્રમણ કરવામાં આવેલો કોણ ($rad$ માં) શું થાય?View Solution
- 8નિયમિત સળિયાનું દળ $ M$ અને લંબાઈ $ ℓ$ સળિયાને લંબ કેન્દ્રમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રા $ I$ છે. સળિયાના છેડામાંથી પસાર થતી અને સળિયાને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 9દળ $m$ અને લંબાઈ $l$ નો એક તાર વર્તુળાકાર રિંગના સ્વરૂપમાં વાળેલો છે, તો તેની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા શું થશે?View Solution
- 10એક રીંગ અને ધન ગોળો સમાન ઢોળાવ પરથી સરક્યા સિવાય ગબડી રહ્યા છે. તેઓ વિરામસ્થિતિમાંથી શરૂ કરે છે. બંને પદાર્થોની ત્રિજ્યાં સમાન છે. તેઓની ગતિઉીર્જાઓનો ગુણોત્તર $\frac{7}{x}$ છે, જ્યાં $x$________થશે.View Solution
