$l$ લંબાઇના સળિયાને ચુંબકીયક્ષેત્રમાં લંબ રાખીને તેના એક છેડાને અનુલક્ષીને $ \omega $ કોણીય ઝડપથી ભ્રમણ કરાવતાં તેના બે છેડા વચ્ચે કેટલો $emf$ ઉત્પન્ન થશે?
Diffcult
a
(a) If in time \(t\). the rod turns by an angle \(\theta\), the area generated by the rotation of rod will be
(a) If in time \(t\). the rod turns by an angle \(\theta\), the area generated by the rotation of rod will be
\( = \frac{1}{2}l \times l\theta \) \( = \frac{1}{2}{l^2}\theta \)
So the flux linked with the area generated by the rotation of rod
\(\phi = B\;\left( {\frac{1}{2}{l^2}\theta } \right)\cos 0 = \frac{1}{2}B{l^2}\theta = \frac{1}{2}B{l^2}\omega \,t\)
And so \(e = \frac{{d\phi }}{{dt}} = \frac{d}{{dt}}\left( {\frac{1}{2}B{l^2}\omega t} \right) = \frac{1}{2}B{l^2}\omega \)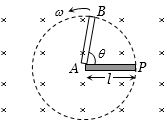
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$100\,cm^2$ ક્ષેત્રફળ અને $50$ આંટા ધરાવતી કોઇલ પર $2 \times 10^{-2}\, T $ જેટલું ચુંબકીય ક્ષેત્ર લંબરૂપે લાગે છે. જ્યારે કોઇલને $t$ સમયમાં ક્ષેત્રની બહાર લઈ જવામાં આવે, ત્યારે પ્રેરિત $emf$ નું મૂલ્ય $0.1\,V$ છે. $t$ નું મૂલ્ય સેકન્ડમાં કેટલું હશે?View Solution
- 2એક લાંબા સોલેનોઇડના આંટાની સંખ્યા $1000 $ છે. જયારે તેમાંથી $4\;A$ નો પ્રવાહ વહેતો હોય, ત્યારે સોલેનોઇડના દરેક આંટા સાથે સંકળાયેલ ફ્લકસ $4 \times10^{-3} \;Wb$ છે. આ સોલેનોઇડનું આત્મપ્રેરકત્વ ....... $H$ હશે?View Solution
- 3$10\, ohm$ અવરોધ ધરાવતા બંધ પરિપથનું ચુંબકીય ફલક્સ સમય સાથે $\phi = 6t^2 - 5t +1$ વેબર મુજબ બદલાય છે. $t = 0.25\, s$ એ પ્રેરિત પ્રવાહનું મૂલ્ય ($A$ માં) કેટલું હશે?View Solution
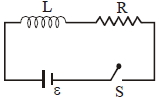
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે $\varepsilon \; emf \;$ ધરાવતી બેટરી સાથે $L$ ઇન્ડક્ટર અને $R$ અવરોધ શ્રેણીમાં જોડેલા છે.$t=0$ સમયે કળ બંધ છે.$\mathrm{t}=0$ અને $\mathrm{t}=\mathrm{t}_{\mathrm{c}}\;( \mathrm{t}_{\mathrm{c}}=$પરિપથનો સમય અચળાંક) વચ્ચે બેટરીમાથી કેટલો વિજભાર બહાર આવ્યો હશે?View Solution
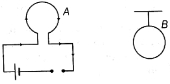
- 5તંત્રમાં બે કોઇલ $A$ અને $B$ છે. કોઇલ $A$ માં અચળ પ્રવાહ $I$ પસાર થાય છે.જ્યારે કોઇલ $B$ ને નજીકમાં મૂકેલી છે, હવે તંત્રને ગરમ કરવામાં આવે છે, તેથી બંન્ને કોઇલનું તાપમાન વધે તો,View Solution
- 6એક વર્તુળાકાર ગુચળામાંથી $I$ પ્રવાહ વહે છે જે ચુંબકીય ડાઈપોલ બનાવે છે.જે અનંત સમતલમાં વર્તુળાકાર ગુચળું છે તે સમતલમાં વર્તુળાકાર ગુચળાના ક્ષેત્રફળને બાદ કરી વધેલા ભાગ માટે ચુંબકીય ફ્લક્સ $\phi_{i}$ છે. વર્તુળાકાર ગુચળાના ક્ષેત્રફળમાથી પસાર થતું ચુંબકીય ફ્લક્સ $\phi_{0}$ હોય તો નીચેનામાથી શું સાચું પડે?View Solution
- 7પ્રાથમિક ગૂંચળામાં આંટાની સંખ્યા $100$ અને ગૌણ ગૂંચળામાં આંટાની સંખ્યા $25$ છે,ગૌણ ગૂંચળામાં પ્રવાહ $4\,A$ છે,જો કાર્યક્ષમતા $100\%$ હોય,તો પ્રાથમિક ગૂંચળામાં પ્રવાહ કેટલા ......$amp$ હશે?View Solution
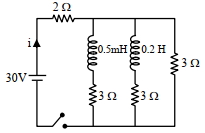
- 8આપેલ પરિપથમાં જ્યારે કળ બંધ કરીને અને સ્થાયી સ્થિતિ પ્રાપ્ત કરે ત્યારે તેમાંથી પસાર થતો પ્રવાહ $i$ ($A$ માં) કેટલો હશે?View Solution
- 9$X Y$ વાહક તાર જમણી બાજુ ખસે છે તે દરમિયાન વિદ્યુત પ્રવાહ વિષમઘટી દિશામાં વહે છે. તો બિંદુ $O$ આગળ યુંબકીય ક્ષેત્રની દિશાView Solution
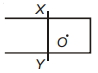
- 10કોઇલમાં પ્રવાહ $8\, A$ થી $2 \,A$ , $ 3 \times {10^{ - 2}} $ $second$ માં કરતાં $2\, V$ $emf$ ઉત્પન્ન થાય છે.તો કોઇલનું આત્મપ્રેરકત્વ કેટલું થાય? (in $millihenry$)View Solution
